31 Gaussian mixture
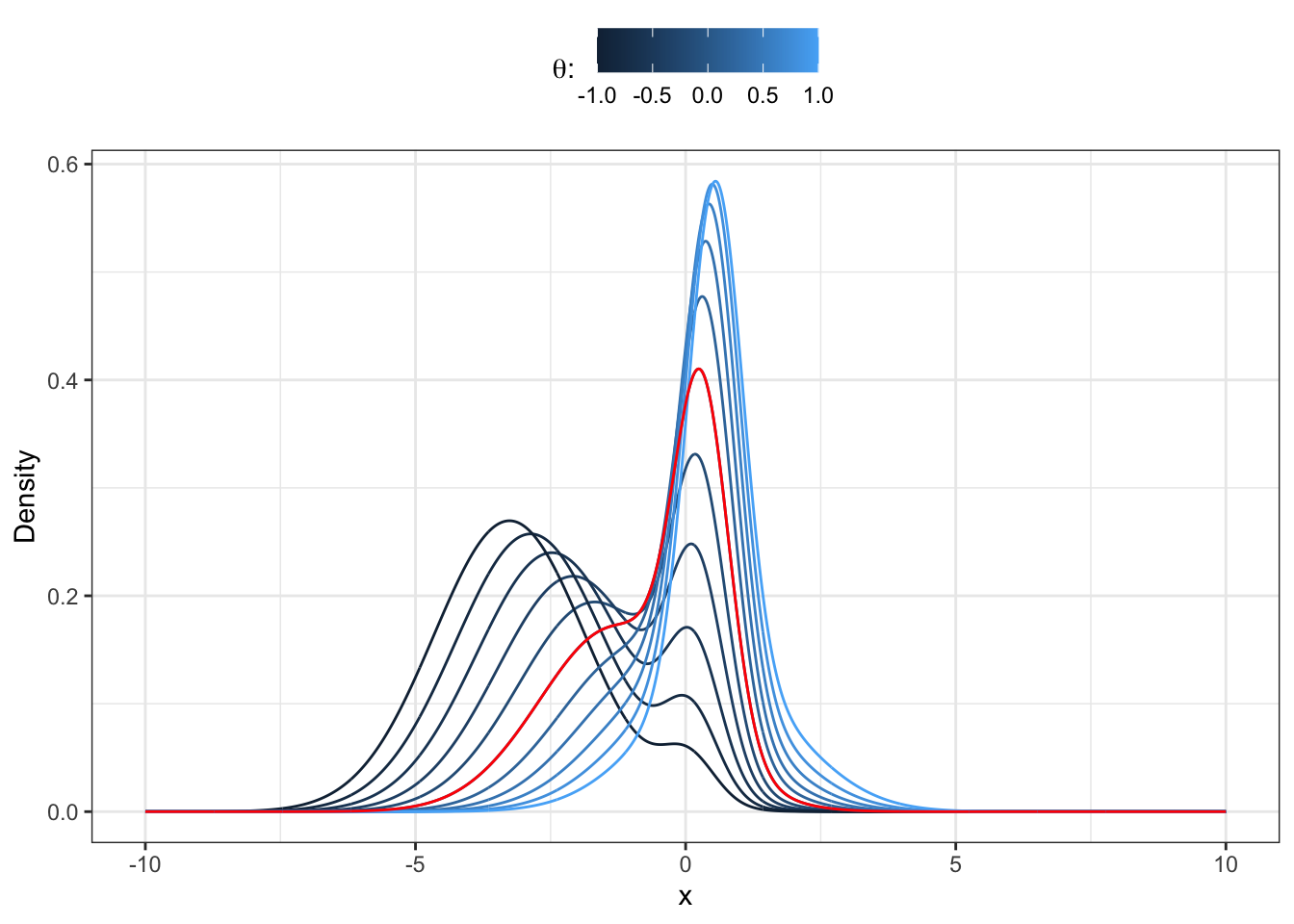
Let’s consider a linear combination of a Bernoulli and two normal random variables, all assumed to be independent, i.e.
31.1 Distribution and density
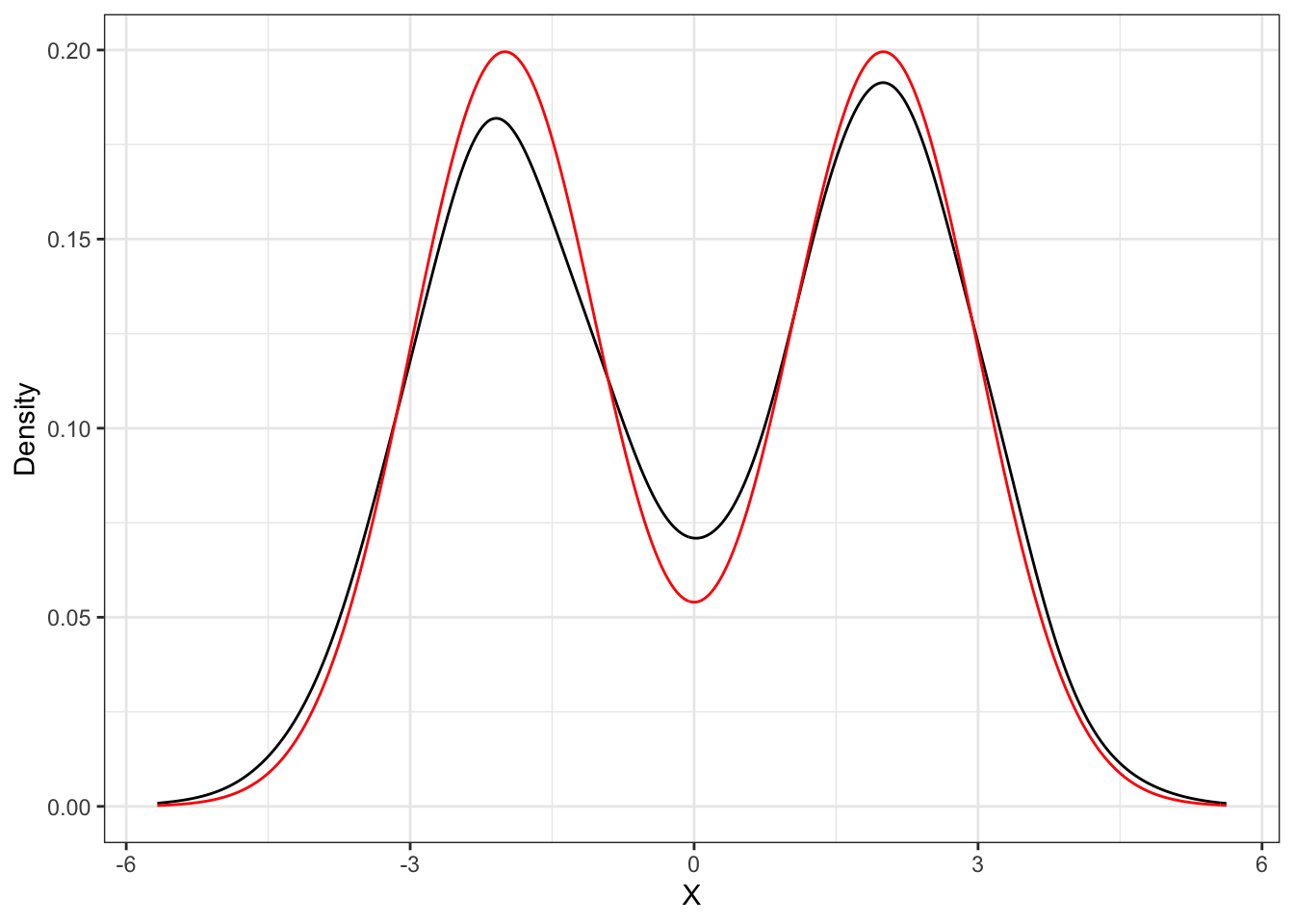
Proposition 31.1 The distribution function of a Gaussian mixture random variable is a weighted sum between the distributions of the components, i.e.: dmixnorm for the density and pmixnorm for the distribution.
Proof. From the formal definition of distribution function of a random variable
31.2 Moment generating function
Proposition 31.2 The moment generating function of a Gaussian mixture random variable (Equation 31.1) in
Proof. Applying the definition of moment generating function and the property of linearity of the expectation on a Gaussian mixture (Equation 31.1), one obtain:
31.3 Esscher transform
Proposition 31.3 The Esscher transform of a Gaussian mixture random variable reads:
Proof. In general, the Esscher transform of a density function
31.4 Moments
Proposition 31.4 The expectation of a Gaussian Mixture random variable (Equation 31.1) reads:
Proof. Given that
31.4.1 Special Cases
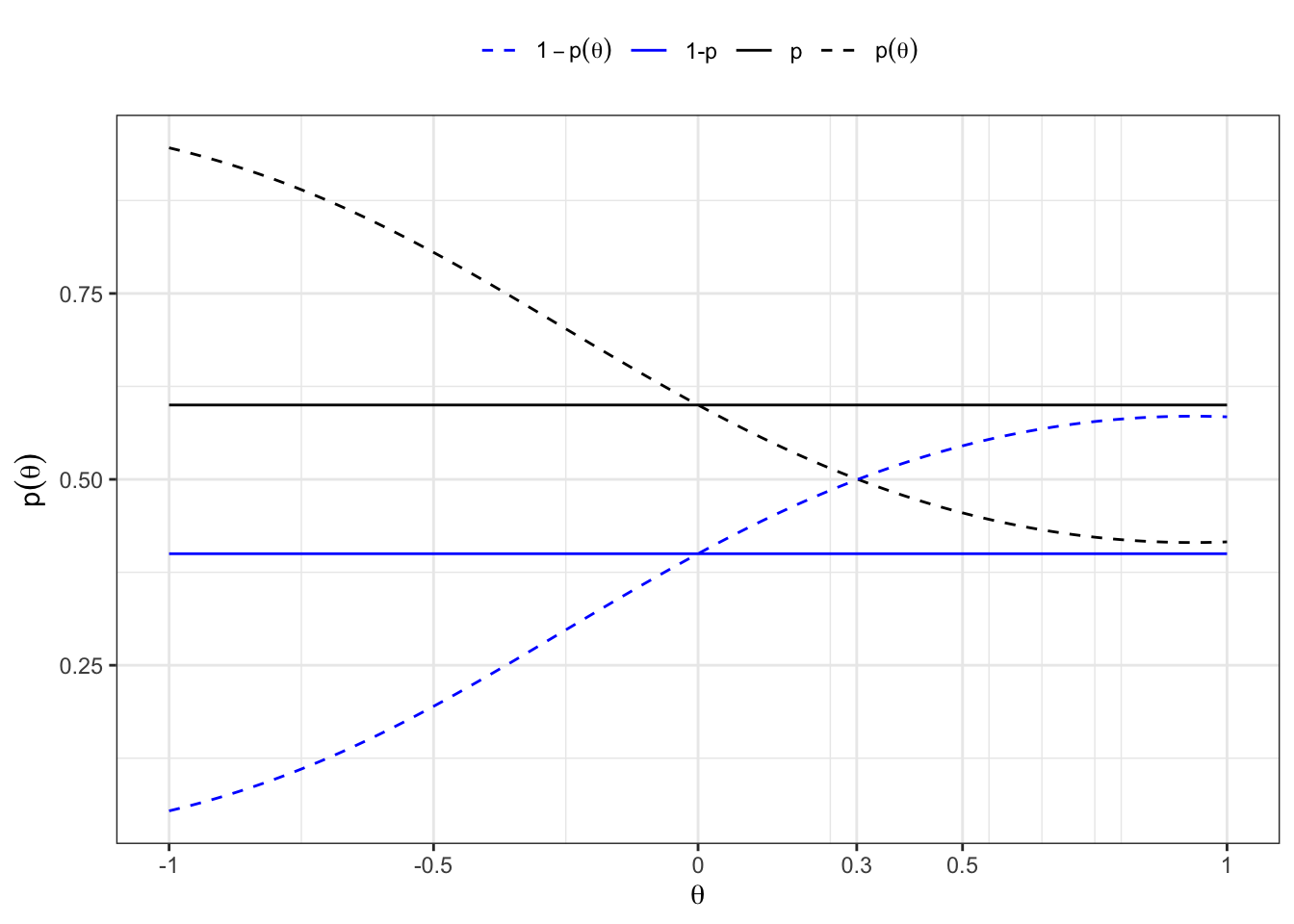
Proposition 31.5 If the random variable
Proof. Let’s show that the following expressions
31.4.2 Central moments
Proposition 31.6 The second central moment of a Gaussian mixture reads:
Proof. Developing the squares:
31.5 Estimation
31.5.1 Maximum likelihood
Minimizing the negative log-likelihood gives an estimate of the parameters, i.e.
Maximum likelihood for Gaussian mixture
# Initialize parameters
init_params <- par*runif(5, 0.3, 1.1)
# Log-likelihood loss function
loss <- function(params, x){
# Parameters
mu1 = params[1]
mu2 = params[2]
sd1 = params[3]
sd2 = params[4]
p = params[5]
# Ensure that probability is in (0,1)
if(p > 0.99 | p < 0.01 | sd1 < 0 | sd2 < 0){ s
return(NA_integer_)
}
# Mixture density
loglik <- function(x) log(dmixnorm(x, params[1:2], params[3:4], c(params[5], 1-params[5])))
# Log-likelihood
sum(loglik(x), na.rm = TRUE)
}
# Optimal parameters
# fnscale = -1 to maximize (or use negative likelihood)
ml_estimate <- optim(par = init_params, loss,
x = Xt, control = list(maxit = 500000, fnscale = -1))31.5.2 Moments matching
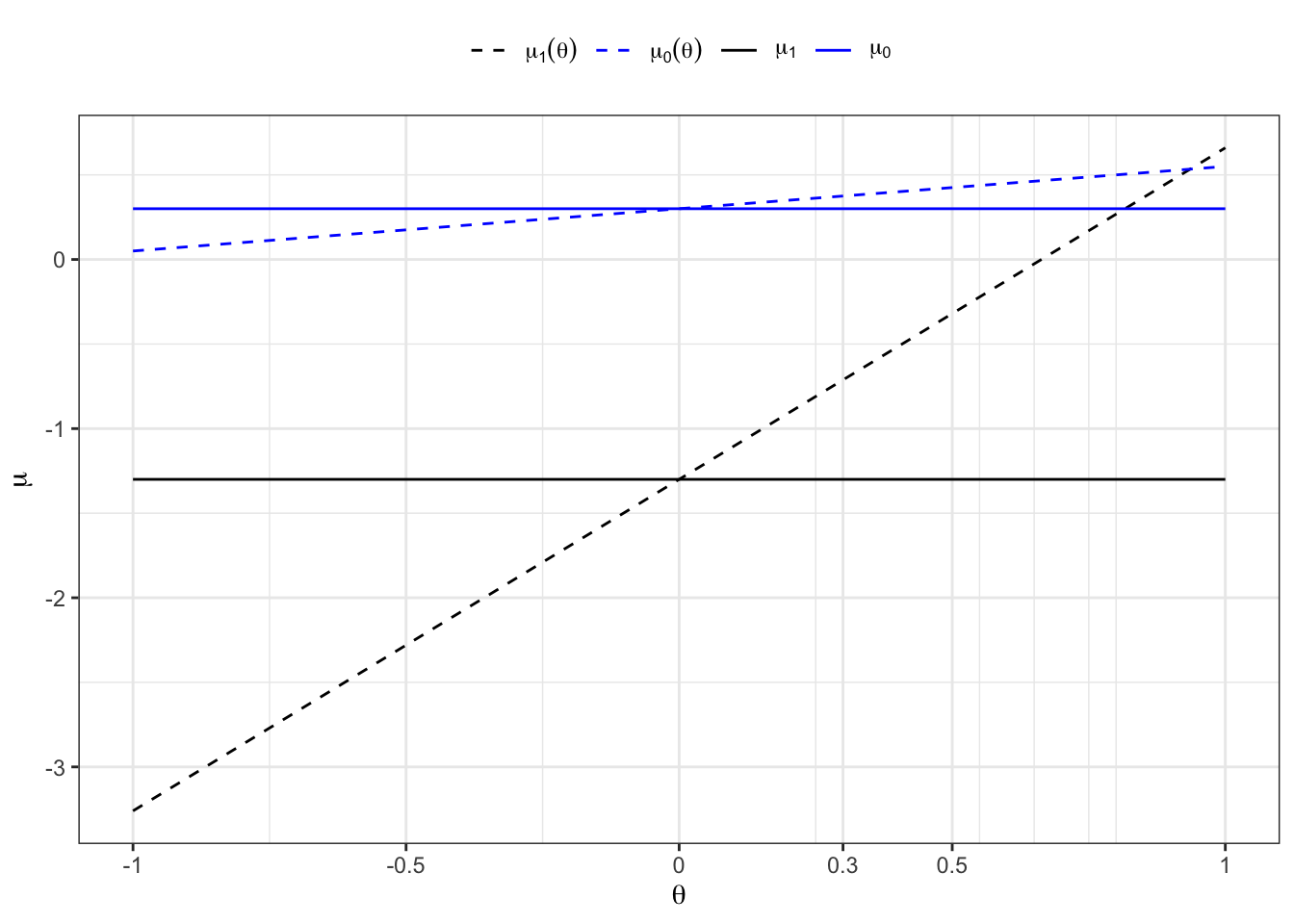
Let’s fix the parameter of the first component, namely
31.5.3 EM
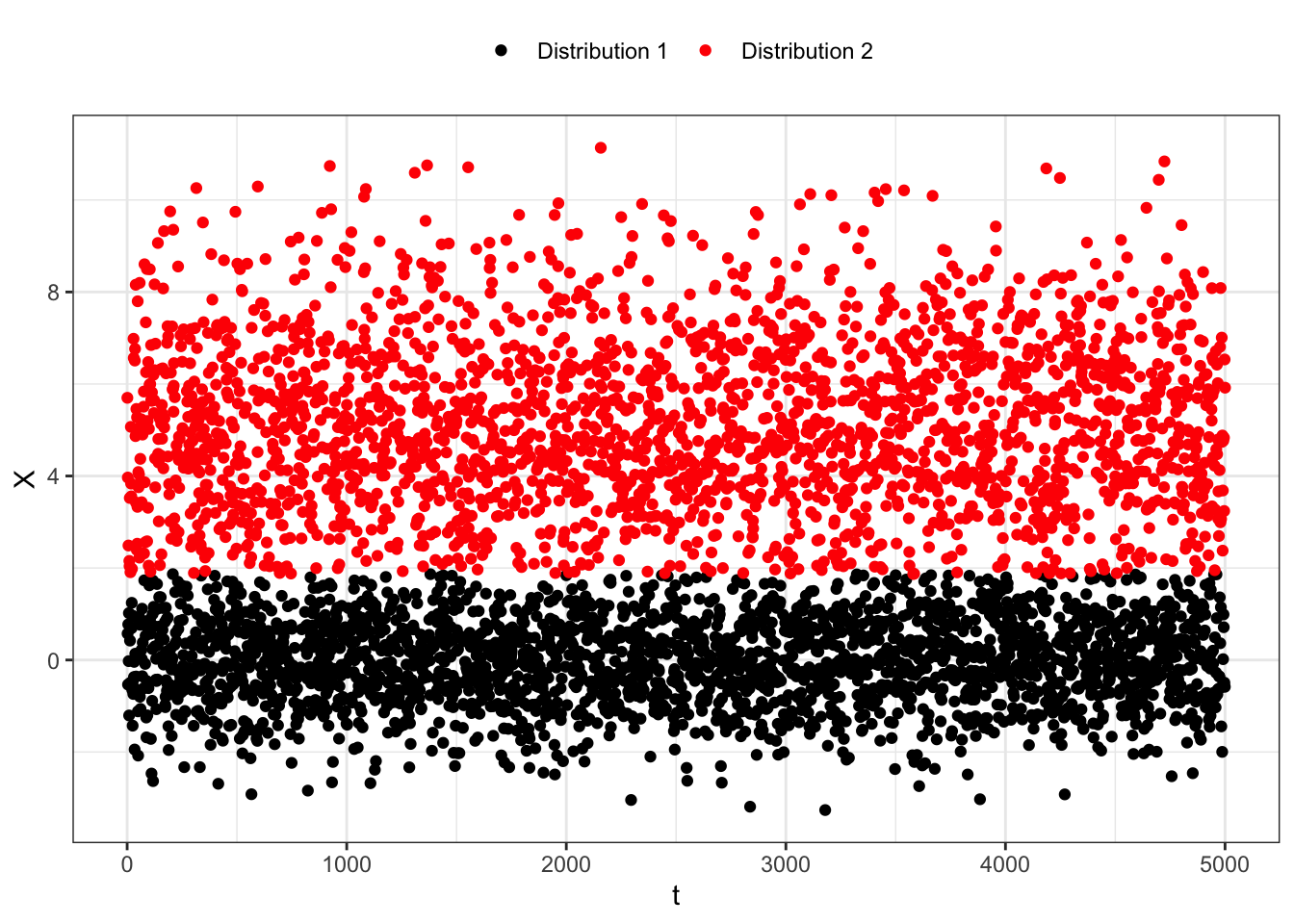
To classify an existing empirical series into two groups (Bernoulli = 0 and Bernoulli = 1) such that the empirical properties (mean and variance) of the groups match the theoretical properties of the original normal distributions, we can use an Expectation-Maximization (EM) algorithm. Here we summarizes the steps and formulas used in the EM algorithm routine to classify an empirical series into two groups such that the empirical properties match the theoretical properties of two normal distributions.
| Step | Description |
|---|---|
| Initialization | Initialize responsibilities and other parameters. |
| 1. E-step | Calculate the responsibilities for each data point as: |
| Compute |
|
| 2. M-step | Update the parameters using the calculated responsibilities: |
| Means: |
|
| Variances: |
|
| Bernoulli probability: |
|
| 3. Log-likelihood | Calculate the log-likelihood for convergence check. |
| 4. Check convergence | Check if the change in log-likelihood is below a threshold, otherwise come back to 1. |
| Output | Series of Bernoulli |
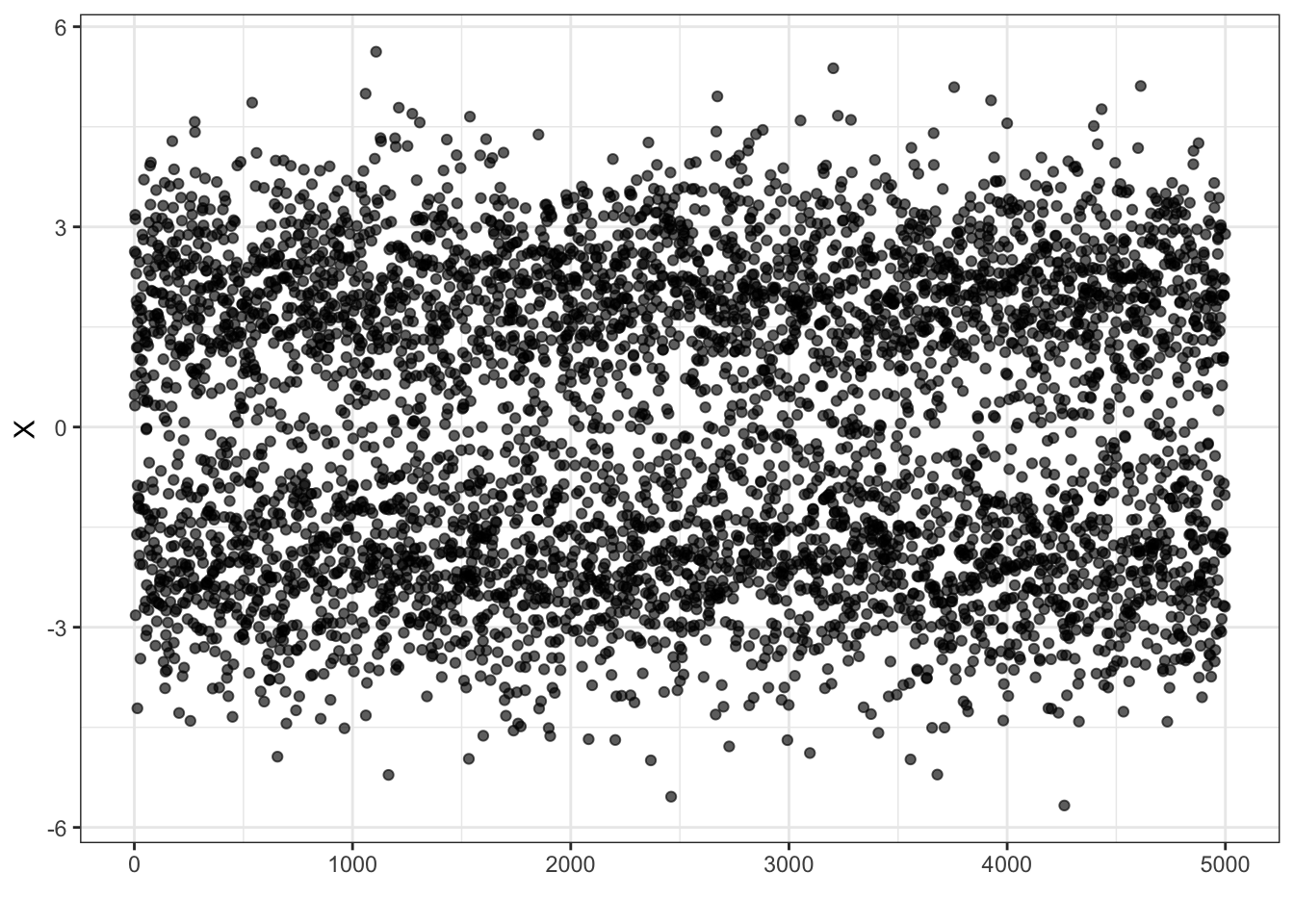
Gaussian Mixture Estimation
# ============================== Inputs ==============================
n <- 5000
# Theoretical parameters
p <- 0.5 # Probability of Bernoulli
# Parameters for the normal distributions
mu1 <- 0 # Mean of the first normal distribution
sigma1 <- 1 # Standard deviation of the first normal distribution
mu2 <- 5 # Mean of the second normal distribution
sigma2 <- 2 # Standard deviation of the second normal distribution
true_params <- c(mu1, mu2, sigma1, sigma2, p)
# ======================================================================
# Generate a random sample
set.seed(123)
# Generate empirical data
B <- rbinom(n, size = 1, prob = p)
Z1 <- rnorm(n, mean = mu1, sd = sigma1)
Z2 <- rnorm(n, mean = mu2, sd = sigma2)
x <- B*Z1 + (1-B)*Z2
# ======================================================================
# Perturb the true parameters
par <- init_params <- true_params*runif(length(true_params), min = 0.8, max = 1.2)
abstol <- 1e-6 # absolute threshold tolerance for convergence
maxit <- 1000 # maximum iteration
match_moments = FALSE # match empirical moments for second distribution
# ======================================================================
# Number of observations
n_ <- length(x)
# Empiric expectation
e_x_emp = mean(x)
# Empiric variance
v_x_emp = var(x)
# Empiric std. deviation
sd_x_emp = sqrt(v_x_emp)
# Initialization
log_likelihood <- 0
previous_log_likelihood <- -Inf
responsibilities <- matrix(0, nrow = n, ncol = 2)
previous_params <- par
# EM Routine
for (iteration in 1:maxit) {
# 1. E-step: Calculate the responsibilities
for (i in 1:n_) {
responsibilities[i, 1] <- previous_params[5] * dnorm(x[i], previous_params[1], previous_params[3])
responsibilities[i, 2] <- (1 - previous_params[5]) * dnorm(x[i], previous_params[2], previous_params[4])
}
# Normalize the probabilities by row
responsibilities <- responsibilities/rowSums(responsibilities)
# 2. M-step: Update the parameters
n1 <- sum(responsibilities[, 1])
n2 <- sum(responsibilities[, 2])
# A) First component
## Means
mu1 <- sum(responsibilities[, 1] * x) / n1 # means
## Std. deviations
sigma1 <- sqrt(sum(responsibilities[, 1] * (x - mu1)^2)/(n1-1)) # std. deviation
# B) Second component
if (match_moments) {
# Match moments approach for (mu2, sigma2)
# Means
mu2 <- (e_x_emp - p * mu1) / (1 - p)
# Std- deviations
sigma2 <- sqrt((v_x_emp - p * sigma1^2) / (1 - p) - p * (mu1 - mu2)^2)
} else {
# Means
mu2 <- sum(responsibilities[, 2] * x) / n2
# Std. deviations
sigma2 <- sqrt(sum(responsibilities[, 2] * (x - mu2)^2) / (n2 - 1))
}
# C) Bernoulli probability
p <- n1 / n_
# 3. Calculate the log-likelihood
log_likelihood <- sum(log(rowSums(responsibilities*cbind(p * dnorm(x, mu1, sigma1), (1 - p) * dnorm(x, mu2, sigma2)))))
# 4. Check for convergence
if (abs(log_likelihood - previous_log_likelihood) < abstol) {
break
}
# Update log-likelihood
previous_log_likelihood <- log_likelihood
# Update parameters
previous_params <- c(mu1, mu2, sigma1, sigma2, p)
}
# ======================================================================
# Output
# Mixture classification
B_hat <- ifelse(responsibilities[, 1] > responsibilities[, 2], 1, 0)
x1_hat <- x[B_hat == 1]
x2_hat <- x[B_hat == 0]
# Optimal parameters
par <- previous_params
# Theoretical moments
e_x_th <- par[1]*par[5] + par[2]*(1-par[5])
sd_x_th <- sqrt(par[5]*(1-par[5])*(par[1] - par[2])^2 + par[3]^2*par[5] + par[4]^2*(1-par[5]))
# Empirical parameters
par_hat <- c(mean(x1_hat), mean(x2_hat), sd(x1_hat), sd(x2_hat), mean(B_hat))
# Empirical moments
e_x_hat <- par_hat[1]*par_hat[5] + par_hat[2]*(1-par_hat[5])
sd_x_hat <- sqrt(par_hat[5]*(1-par_hat[5])*(par_hat[1] - par_hat[2])^2 + par_hat[3]^2*par_hat[5] + par_hat[4]^2*(1-par_hat[5]))
# ======================================================================
# Dataset containing classified series
data = dplyr::tibble(B = B_hat, x = x, x1 = x*B, x2 = x*(1-B))
# Dataset containing initial, optimal, empirical and true parameters
params = tibble(param = c("mu1","mu2","sd1","sd2","p"),
init = init_params,
opt = par,
hat = par_hat,
true = true_params)
# Dataset containing empirical and theoretical moments series
moments = tibble(statistic = c("Mean", "Std. Dev"),
emp = c(e_x_emp, sd_x_emp),
opt = c(e_x_th, sd_x_th),
hat = c(e_x_hat, sd_x_hat))31.5.4 Matrix moments matching
Proposition 31.7 Any finite K-component Gaussian mixture with finite moments admits a more parsimonious moment-matching approximation with only two-component Gaussian mixture. We start with the parameters of the mixture at time
Proof. Let’s consider the following approach. We start by fixing the mixture probabilities at time