21 Conditional variance processes
A stochastic process for the conditional variance can be used to specify a model of the form
21.1 ARCH(p) process
The auto regressive and conditionally heteroskedastic process (ARCH) were introduced in 1982 by Robert Engle (Engle (1982)) to model the conditional variance of a time series. It is often an empirical fact in economics that the larger values of time series the larger the variance. Let’s define an ARCH process of order
21.1.1 Moments
Proposition 21.1 The conditional mean of an ARCH(p) process (Equation 21.1) is equal to
Proposition 21.2 The conditional variance of an ARCH(p) process (Equation 21.1) is not stochastic given the information at time
The long-term (unconditional) expectation of the ARCH(p) variance
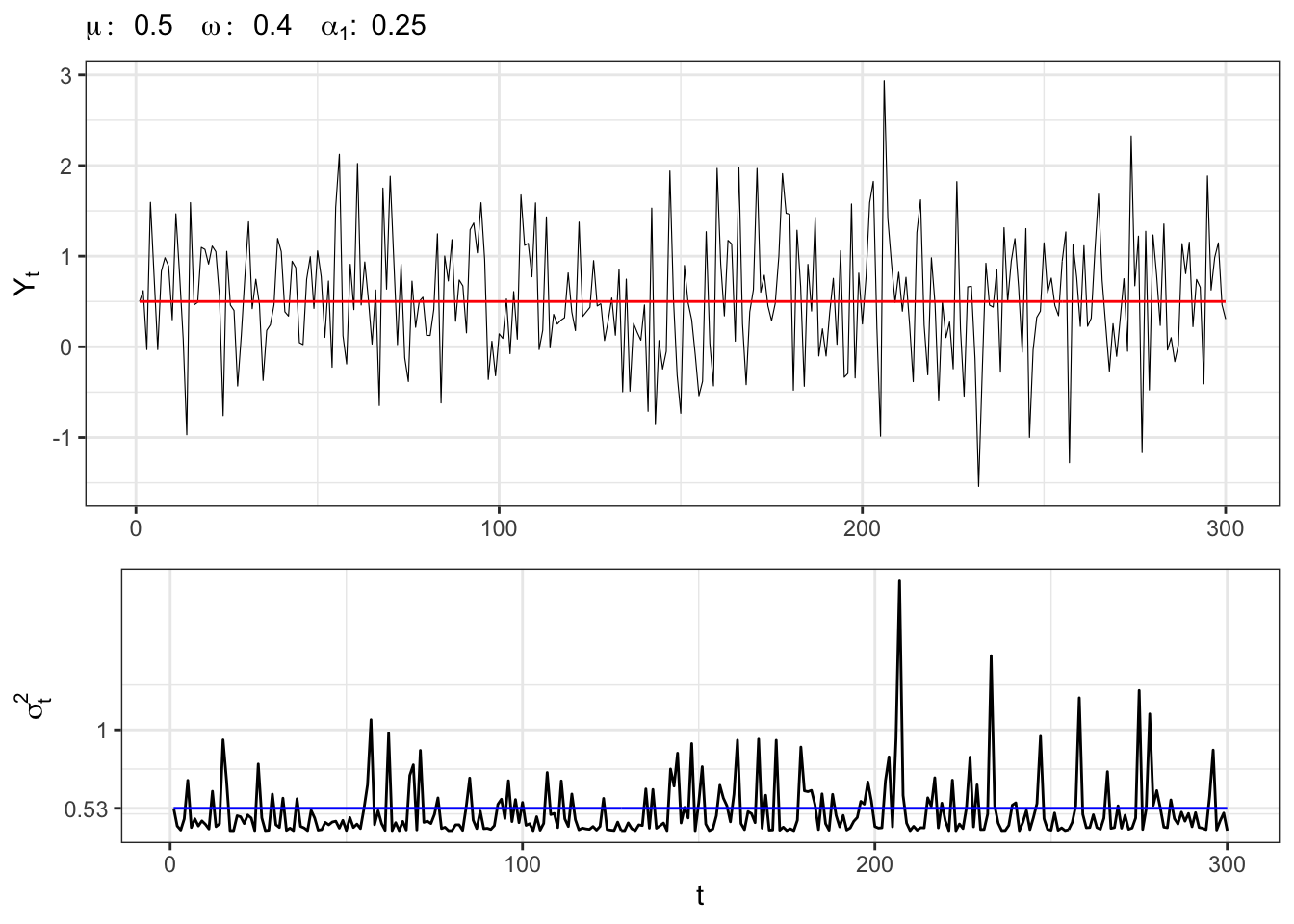
Example 21.1 Let’s simulate an ARCH(1) process with normal residuals, i.e.
ARCH(1) simulation
# Random seed
set.seed(1)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.4
# ARCH parameters
alpha <- c(alpha1 = 0.25)
# *************************************************
# Simulation
# *************************************************
# Long-term variance
e_sigma2 <- omega / (1 - sum(alpha))
# Starting point
Yt <- rep(mu, 2)
# Initialization
sigma2_t <- rep(e_sigma2, 4)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 2:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2
# Next-step variance
sigma2_t[t] <- omega + sum_arch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + e_t[t]
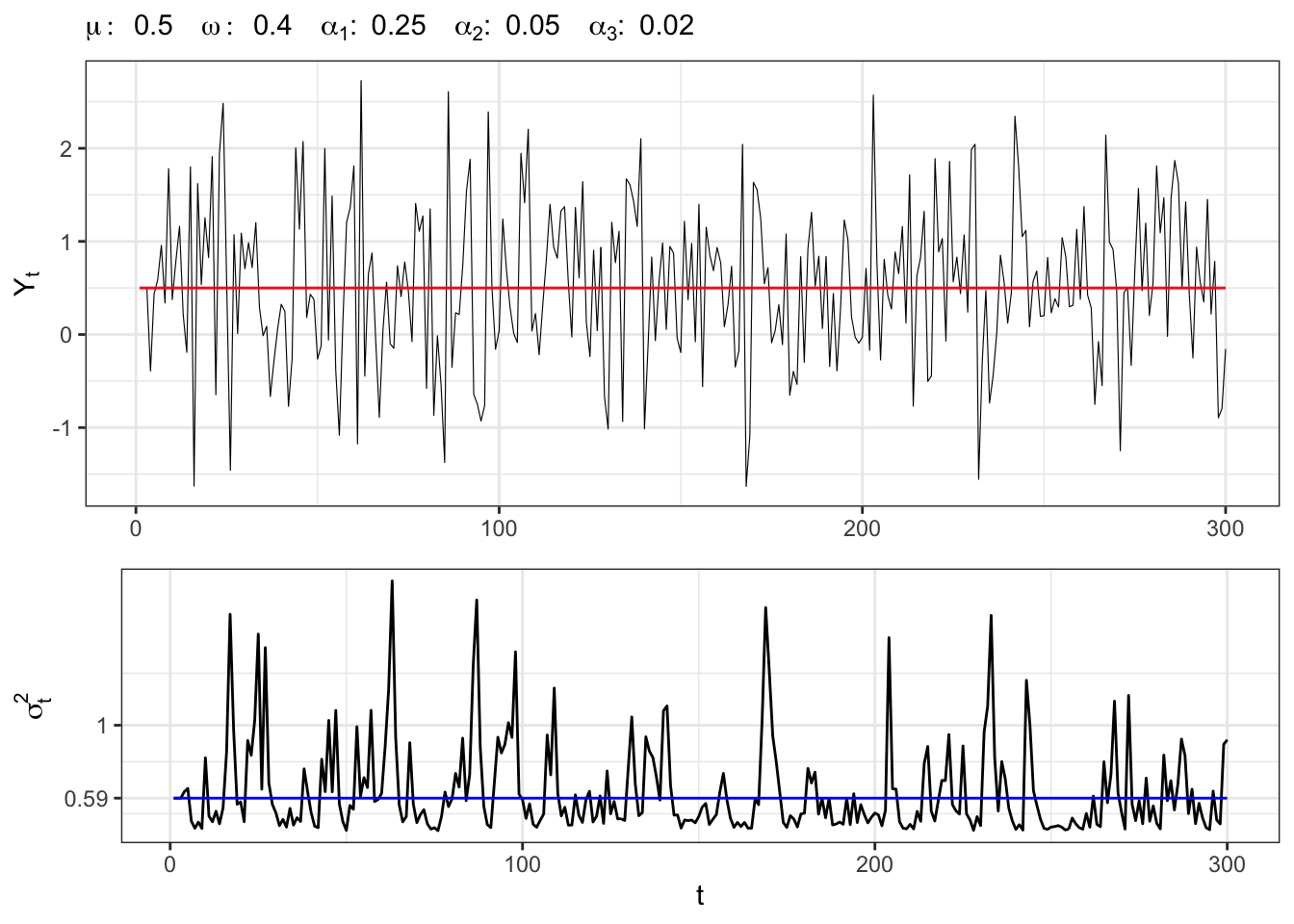
}Example 21.2 Let’s simulate an ARCH(3) process with normal residuals, i.e.
ARCH(3) simulation
# Random seed
set.seed(2)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.4
# ARCH parameters
alpha <- c(alpha1 = 0.25, alpha2 = 0.05, alpha3 = 0.02)
# *************************************************
# Simulation
# *************************************************
# Long-term variance
e_sigma2 <- omega / (1 - sum(alpha))
# Starting point
Yt <- rep(mu, 4)
# Initialization
sigma2_t <- rep(e_sigma2, 4)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 4:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2 + alpha[2] * e_t[t-2]^2 + alpha[3] * e_t[t-3]^2
# Next-step variance
sigma2_t[t] <- omega + sum_arch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + e_t[t]
}21.2 GARCH(p,q) process
As done with the ARCH(p), with generalized auto regressive conditional heteroskedasticity (GARCH) we model the dependency of the conditional second moment. It represents a more parsimonious way to express the conditional variance. A GARCH(p,q) processx is defined as:
Regarding the variance, the long-term expectation of
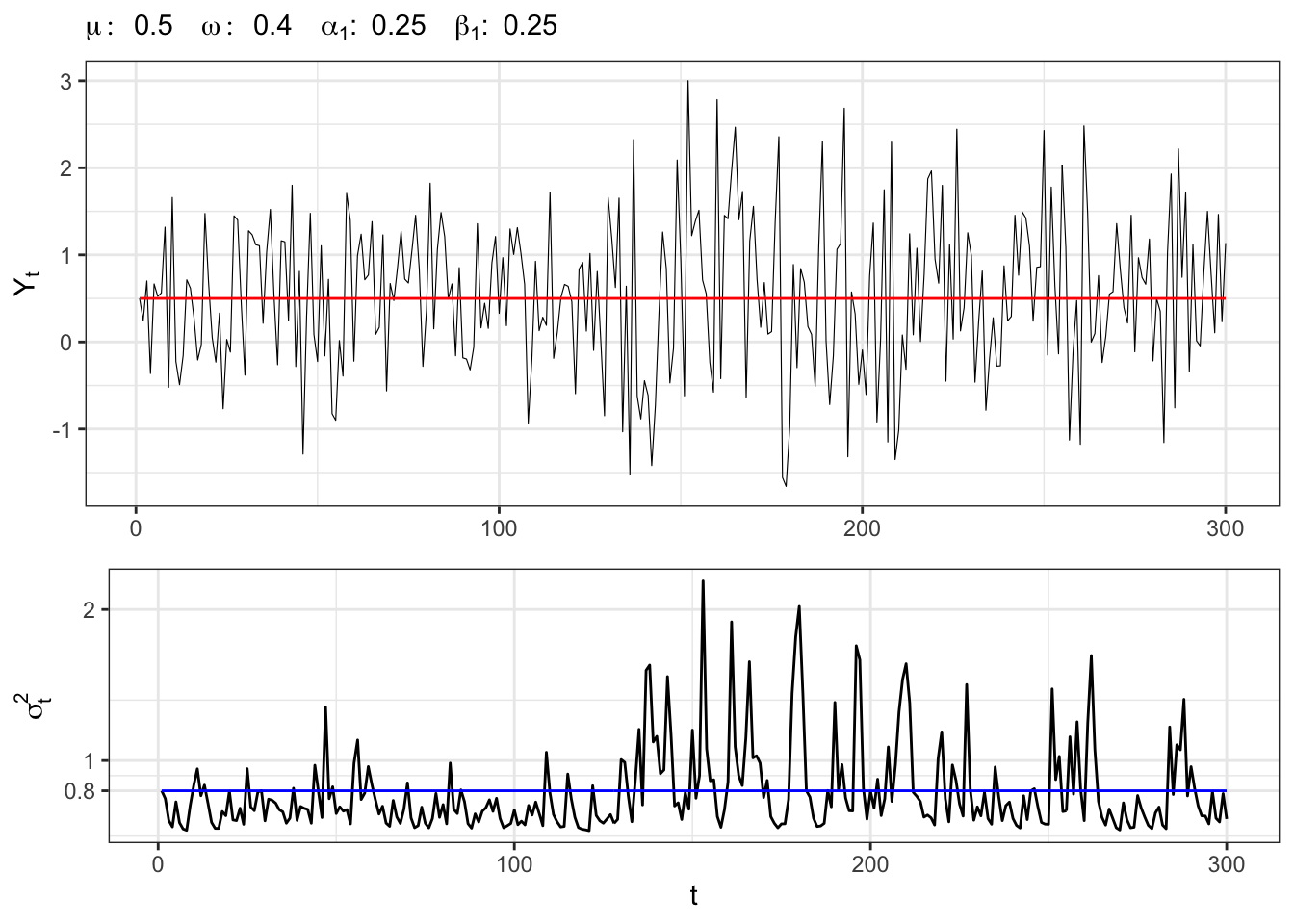
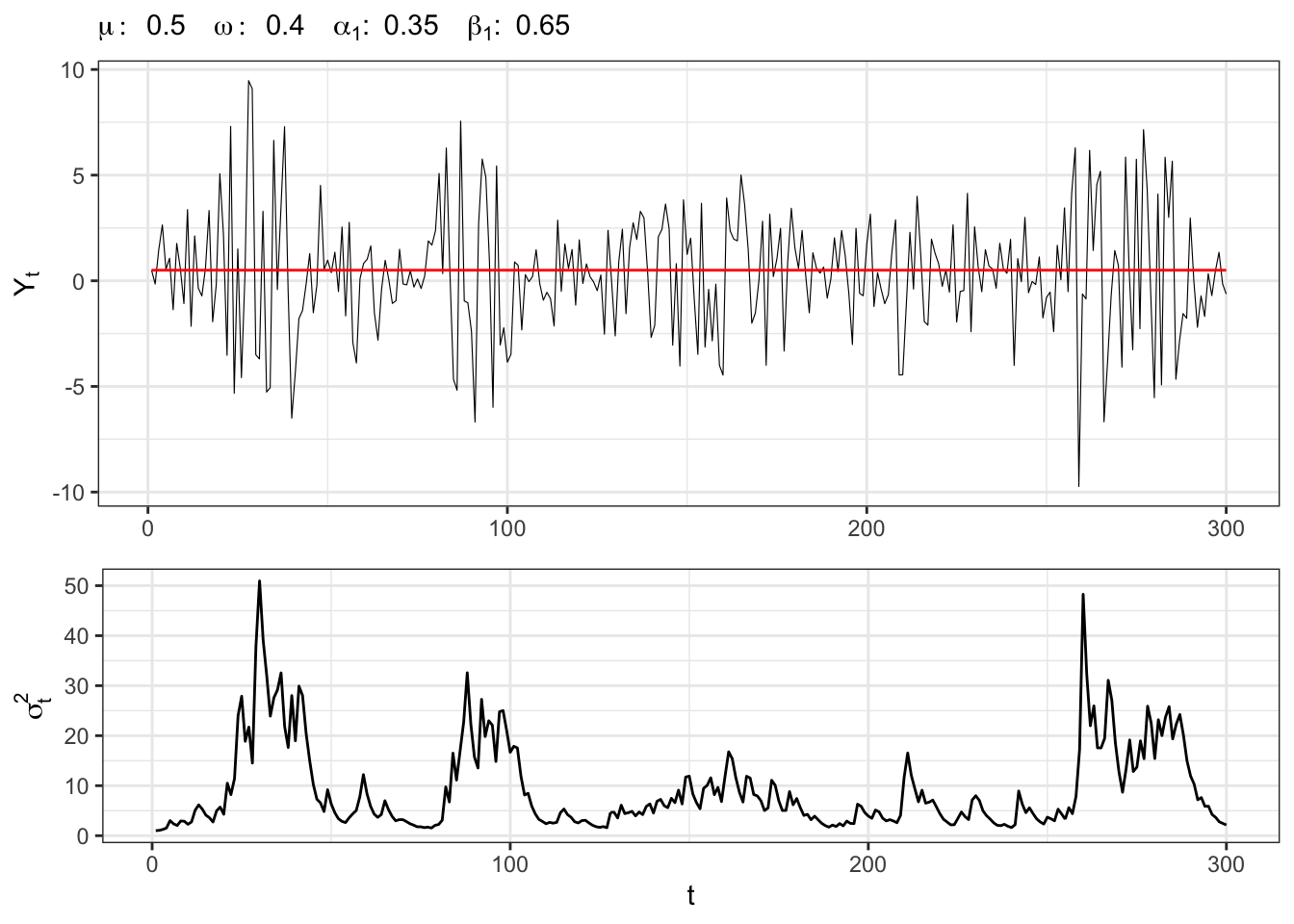
Example 21.3 Let’s simulate an GARCH(1,1) process with normal residuals, i.e.
GARCH(1,1) simulation
# Random seed
set.seed(3)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.4
# ARCH parameters
alpha <- c(alpha1 = 0.25)
# GARCH parameters
beta <- c(beta1 = 0.25)
# *************************************************
# Simulation
# *************************************************
# Long-term variance
e_sigma2 <- omega / (1 - sum(alpha) - sum(beta))
# Starting point
Yt <- rep(mu, 2)
# Initialization
sigma2_t <- rep(e_sigma2, 4)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 2:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2
# GARCH components
sum_garch <- beta[1] * sigma2_t[t-1]
# Next-step variance
sigma2_t[t] <- omega + sum_arch + sum_garch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + e_t[t]
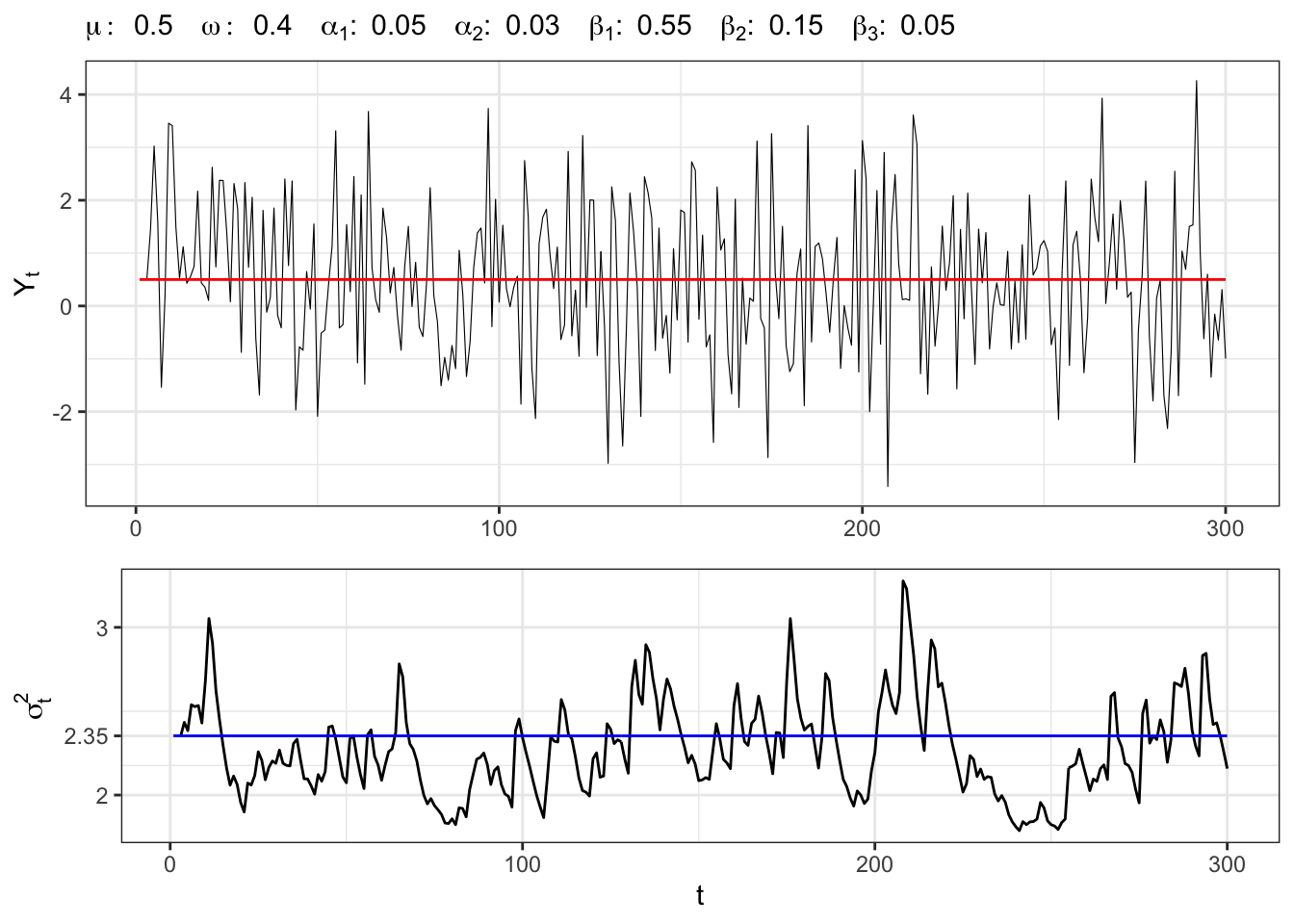
}Example 21.4 Let’s simulate a GARCH(2,3) process with normal residuals, i.e
GARCH(2,3) simulation
# Random seed
set.seed(4)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.4
# ARCH parameters
alpha <- c(alpha1 = 0.05, alpha2 = 0.03)
# GARCH parameters
beta <- c(beta1 = 0.55, beta2 = 0.15, beta3 = 0.05)
# *************************************************
# Simulation
# *************************************************
# Long-term variance
e_sigma2 <- omega / (1 - sum(alpha) - sum(beta))
# Starting point
Yt <- rep(mu, 4)
# Initialization
sigma2_t <- rep(e_sigma2, 4)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 4:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2 + alpha[2] * e_t[t-2]^2
# GARCH components
sum_garch <- beta[1] * sigma2_t[t-1] + beta[2] * sigma2_t[t-2] + beta[3] * sigma2_t[t-3]
# Next-step variance
sigma2_t[t] <- omega + sum_arch + sum_garch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + e_t[t]
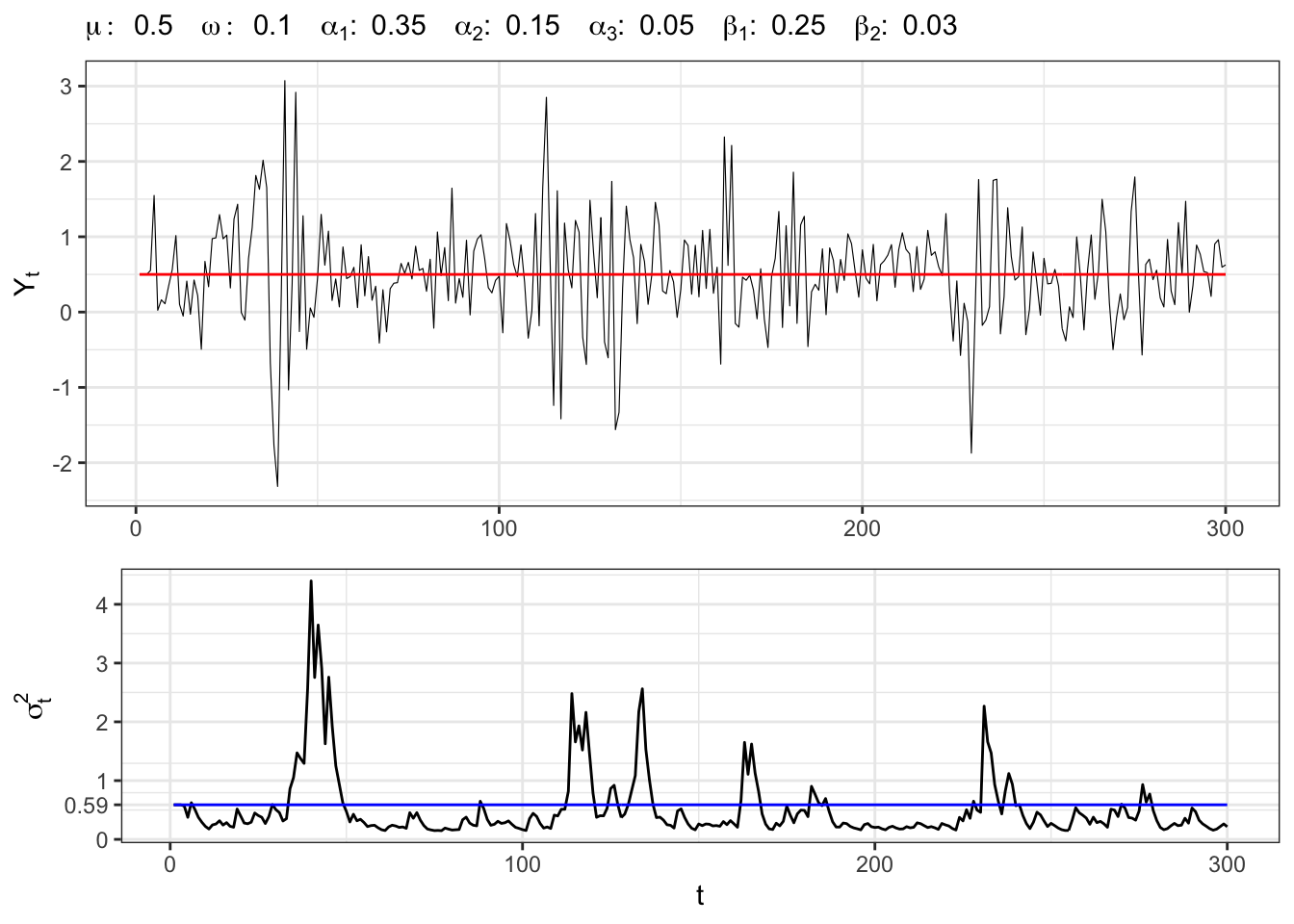
}Example 21.5 Let’s simulate a GARCH(3,2) process with normal residuals, i.e.
GARCH(3,2) simulation
# Random seed
set.seed(5)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.1
# ARCH parameters
alpha <- c(alpha1 = 0.35, alpha2 = 0.15, alpha3 = 0.05)
# GARCH parameters
beta <- c(beta1 = 0.25, beta2 = 0.03)
# *************************************************
# Simulation
# *************************************************
# Long-term variance
e_sigma2 <- omega / (1 - sum(alpha) - sum(beta))
# Starting point
Yt <- rep(mu, 4)
# Initialization
sigma2_t <- rep(e_sigma2, 4)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 4:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2 + alpha[2] * e_t[t-2]^2 + alpha[3] * e_t[t-3]^2
# GARCH components
sum_garch <- beta[1] * sigma2_t[t-1] + beta[2] * sigma2_t[t-2]
# Next-step variance
sigma2_t[t] <- omega + sum_arch + sum_garch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + e_t[t]
}21.3 IGARCH
Many variants of the standard GARCH process were developed in literature. For example, the Integrated Generalized Auto regressive Conditional heteroskedasticity (IGARCH(p,q)) is a restricted version of the GARCH, where the persistent parameters sum up to one, and imply a unit root in the GARCH process with the condition
Example 21.6 Let’s simulate an iGARCH(1,1) process with normal residuals, i.e.
iGARCH(1,1) simulation
# Random seed
set.seed(6)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.4
# ARCH parameters
alpha <- c(alpha1 = 0.35)
# *************************************************
# Simulation
# *************************************************
# Starting point
Yt <- rep(mu, 2)
# Initialization
sigma2_t <- rep(1, 2)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 2:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2
# GARCH components
sum_garch <- (1 - alpha[1]) * sigma2_t[t-1]
# Next-step variance
sigma2_t[t] <- omega + sum_arch + sum_garch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + e_t[t]
}21.4 GARCH-M
The GARCH in-mean (GARCH-M) model adds a stochastic term into the mean equation. This is motivated especially in financial theories (e.g., risk-return trade-off) suggesting that expected returns may depend on volatility, i.e.
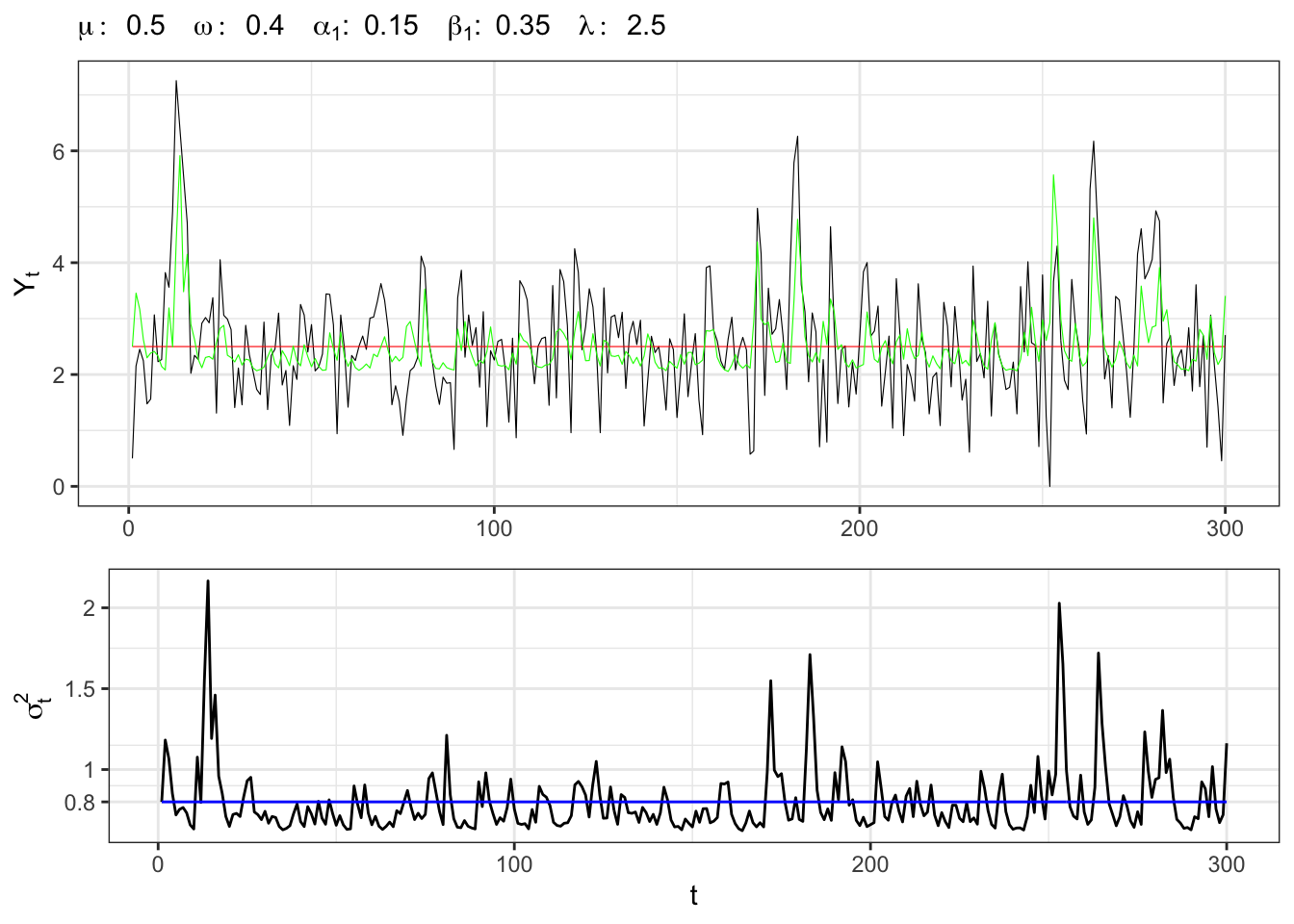
Example 21.7 Let’s simulate an GARCH-M(1,1) process with normal residuals, i.e.
GARCH-M(1,1) simulation
# Random seed
set.seed(7)
# *************************************************
# Inputs
# *************************************************
# Number of simulations
t_bar <- 300
# Long term mean of Yt
mu <- 0.5
# Intercept sigma2
omega <- 0.4
# ARCH parameters
alpha <- c(alpha1 = 0.15)
# Mean param
lambda <- 2.5
# GARCH parameters
beta <- c(beta1 = 0.35)
# *************************************************
# Simulation
# *************************************************
# Long-term variance
e_sigma2 <- omega / (1 - sum(alpha) - sum(beta))
# Starting point
Yt <- rep(mu, 2)
# Initialization
sigma2_t <- rep(e_sigma2, 4)
# Simulate standardized residuals
u_t <- rnorm(t_bar, 0, 1)
# Initialize residuals
e_t <- sigma2_t * u_t
for(t in 2:t_bar){
# ARCH components
sum_arch <- alpha[1] * e_t[t-1]^2
# GARCH components
sum_garch <- beta[1] * sigma2_t[t-1]
# Next-step variance
sigma2_t[t] <- omega + sum_arch + sum_garch
# Update simulated residuals
e_t[t] <- sqrt(sigma2_t[t]) * u_t[t]
# Update time series
Yt[t] <- mu + sigma2_t[t] * lambda + e_t[t]
}