23 Stationarity tests
23.1 Dickey–Fuller test
The Dickey–Fuller test tests the null hypothesis that a unit root is present in an auto regressive (AR) model. The alternative hypothesis is different depending on which version of the test is used, usually is “stationary” or “trend-stationary”. Let’s consider an AR(1) model, i.e. \[ X_t = \mu + \delta t + \phi X_{t-1} + u_t \text{,} \tag{23.1}\] or equivalently adding and subtracting \(X_{t-1}\) \[ \Delta X_t = \mu + \delta t + (1-\phi) X_{t-1} + u_t \text{,} \tag{23.2}\] where \(\Delta X_t = X_t - X_{t-1}\).
The set of hypothesis of the Dickey–Fuller test are: \[ \begin{aligned} & {} \mathcal{H}_0: \phi = 1 \iff (X_t \text{ is non stationarity}) \\ & \mathcal{H}_1: \phi < 1 \iff (X_t \text{ is stationarity}) \end{aligned} \] The Dickey–Fuller statistic is computed as \[ \text{DF} = \frac{1-\hat{\phi}}{\mathbb{S}d\{1-\hat{\phi}\}} \text{.} \] where \(\hat{\phi}\) is the estimated parameter from the regression in Equation 23.3 and \(\mathbb{S}d\{\hat{\phi}\}\) its standard error. However, since the test is done over the residual terms rather than raw data, it is not possible to use the t-distribution to provide critical values and the statistic has its specific distribution.
23.2 Augmented Dickey–Fuller test
The augmented Dickey–Fuller is a more general version of the Dickey–Fuller test for a general AR(p) model, i.e. \[ \Delta X_t = \mu + \delta t + \phi X_{t-1} + \sum_{i = 1}^{p} \phi_i \Delta X_{t-i} \text{.} \tag{23.3}\] The set of hypothesis of the augmented Dickey–Fuller test are: \[ \begin{aligned} & {} \mathcal{H}_0: \phi = 0 \iff (X_t \text{ is non stationarity}) \\ & \mathcal{H}_1: \phi < 0 \iff (X_t \text{ is stationarity}) \end{aligned} \] The augmented Dickey–Fuller statistic (ADF) is computed as: \[ \text{ADF} = \frac{\hat{\phi}}{\mathbb{S}d\{\hat{\phi}\}} \text{.} \] where \(\hat{\phi}\) is the estimated parameter from the regression in Equation 23.3 and \(\mathbb{S}d\{\hat{\phi}\) its relative standard error. As in the Dickey–Fuller test, the critical values are computed using a specific table.
23.3 Kolmogorov-Smirnov test
The Kolmogorov–Smirnov two-sample test (KS) can be used to test whether two samples came from the same distribution. Let’s define the empirical distribution function \(F_{n}\) of \(n\)-independent and identically distributed ordered observations \(x_{(i)}\) as \[ \hat{F}_{\mathbf{x}_n}(x) = \frac{1}{n}\sum_{i = 1}^{n} \mathbb{1}_{(-\infty, x]}(x_{(i)}) \text{.} \tag{23.4}\] The KS statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution functions of two random samples. The distribution of the KS statistic under the null hypothesis assumes that the samples are drawn from the same distribution, i.e. \[ \begin{aligned} & {} \mathcal{H}_0: X_t \text{ is stationary} \\ & \mathcal{H}_1: X_t \text{ is not stationary} \end{aligned} \] The statistic test for two samples with dimension \(n_1\) and \(n_2\) is defined as: \[ \text{KS}(\mathbf{x}_{n_1}, \mathbf{x}_{n_2}) = \underset{\forall x}{\sup}|F_{\mathbf{x}_{n_1}}(x) - F_{\mathbf{x}_{n_2}}(x)| \text{,} \] and for large samples \(\mathcal{H}_0\) is rejected with confidence level \(1 - \alpha\) if: \[ \text{KS}(\mathbf{x}_{n_1}, \mathbf{x}_{n_2}) > \sqrt{-\frac{1}{2n_2} \ln\left(\frac{\alpha}{2}\right) \left(1 + \frac{n_2}{n_1}\right)} \text{.} \] Hence, since the statistic is always greater of equal to zero, with a given statistic \(\text{KS}_{n_1, n_2}\) the p-value with confidence level \(\alpha = 2 \mathbb{P}(X > \text{KS}_{n_1, n_2})\) reads: \[ \mathbb{P}(X > \text{KS}(\mathbf{x}_{n_1}, \mathbf{x}_{n_2})) = \exp\left(- \frac{2 n_2}{1 + \frac{n1}{n2}} \text{KS}(\mathbf{x}_{n_1}, \mathbf{x}_{n_2})^2 \right) \text{.} \]
Example 23.1 Let’s consider 500 simulated observations of the random variable \(X\) drown from a population distributed as \(X \sim N(0.4, 1)\). Then, considering it as a time series, let’s sample a random index to split the series in a point. Finally, as shown in Table 23.1 the null hypothesis, i.e. the two samples come from the same distribution, is not reject with the confidence level \(\alpha = 5\%\).
KS-test on a stationary time series
# ================ Setups ================
set.seed(5) # random seed
ci <- 0.05 # confidence level (alpha)
n <- 500 # number of simulations
x <- rnorm(n, 0.4, 1) # stationary series
# ========================================
# Random time for splitting
t_split <- sample(n, 1)
# Split the time series
x1 <- x[1:t_split]
x2 <- x[(t_split+1):n]
# Number of elements for each sub-series
n1 <- length(x1)
n2 <- length(x2)
# Grid of values for computing KS-statistic
x_min <- quantile(x, 0.015)
x_max <- quantile(x, 0.985)
grid <- seq(x_min, x_max, length.out = 200)
# Empirical cdfs
cdf_n1 <- ecdf(x1)
cdf_n2 <- ecdf(x2)
# KS-statistic
ks_stat <- max(abs(cdf_n1(grid) - cdf_n2(grid)))
# Rejection level with probability alpha
rejection_lev <- sqrt(-0.5*log(ci/2))*sqrt((n1+n2)/(n1*n2))
# P-value
p.value <- exp(- (2 * n2) / (1 + n1/n2) * ks_stat^2)KS-test plot
y_breaks <- seq(0, 1, 0.2)
y_labels <- paste0(format(y_breaks*100, digits = 2), "%")
grid_max <- grid[which.max(abs(cdf_n1(grid) - cdf_n2(grid)))]
ggplot()+
geom_ribbon(aes(grid, ymax = cdf_n1(grid), ymin = cdf_n2(grid)),
alpha = 0.5, fill = "green") +
geom_line(aes(grid, cdf_n1(grid)))+
geom_line(aes(grid, cdf_n2(grid)), color = "red")+
geom_segment(aes(x = grid_max, xend = grid_max, y = cdf_n1(grid_max), yend = cdf_n2(grid_max)),
linetype = "solid", color = "magenta")+
geom_point(aes(grid_max, cdf_n1(grid_max)), color = "magenta")+
geom_point(aes(grid_max, cdf_n2(grid_max)), color = "magenta")+
scale_y_continuous(breaks = y_breaks, labels = y_labels)+
labs(x = "x", y = "cdf")+
theme_bw()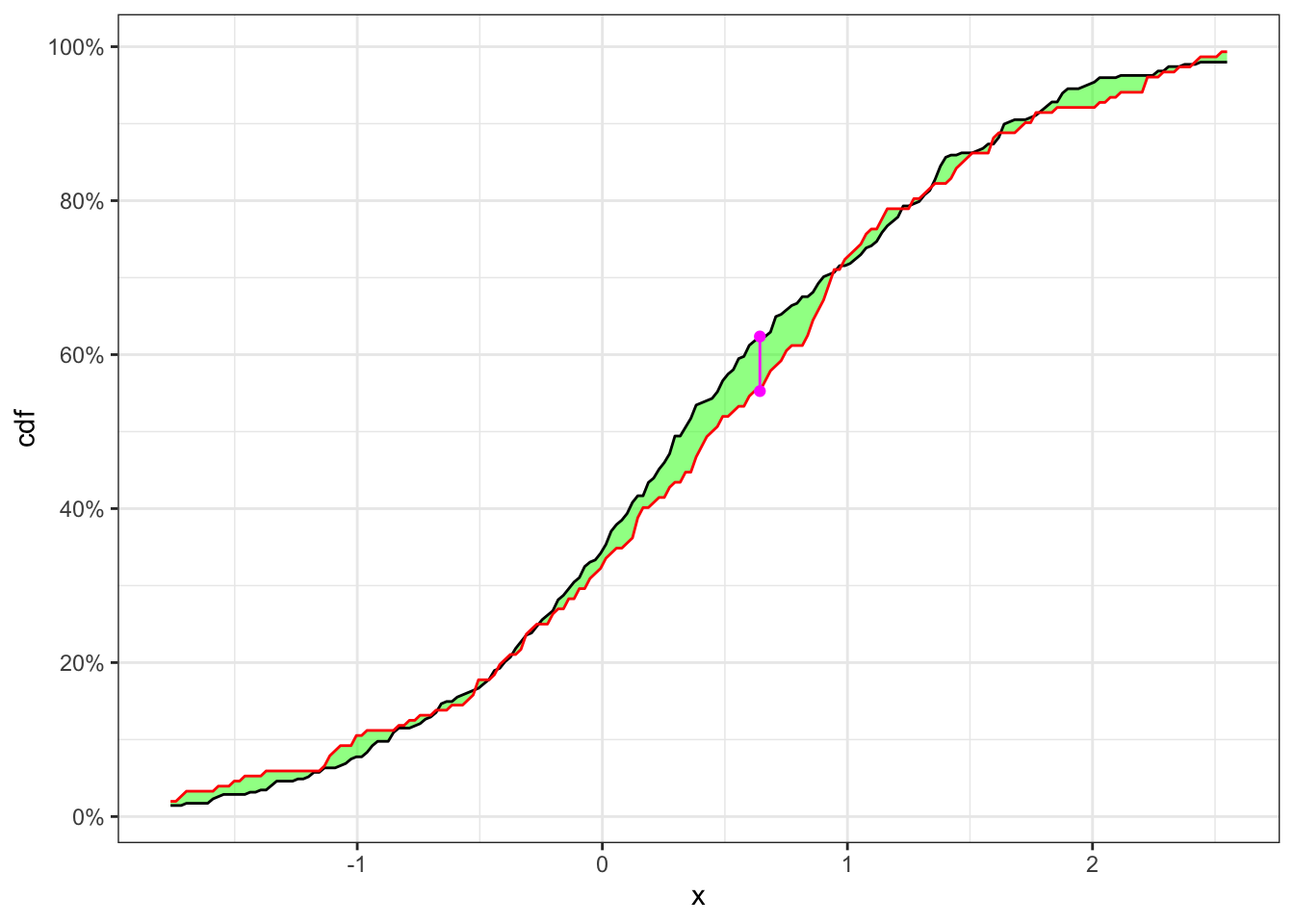
| \(\textbf{Index split}\) | \(\alpha\) | \(n_1\) | \(n_2\) | \(\text{KS}(\mathbf{x}_{n_1}, \mathbf{x}_{n_2})\) | p.value | \(\textbf{Critical level}\) | \(\mathcal{H}_0\) |
|---|---|---|---|---|---|---|---|
| 348 | 0.05 | 348 | 152 | 0.07093 | 0.6282 | 0.132 | Non-Rejected |
Example 23.2 Let’s consider 250 simulated observations of the random variable \(X\) drown from a population distributed as \(Y_{1,t} \sim N(0, 1)\) and the following 250 from \(Y_{2,t} \sim N(0.3, 1)\). Then the non-stationary series will have a structural break at the point 250 and the time series is given by: \[ X_t = \begin{cases} Y_{1,t} \quad t \le 250 \\ Y_{2,t} \quad t > 250 \end{cases} \] As in Example 23.2 let’s split the time series and apply the KS-test. In this case, as shown in Table 23.2 the null hypothesis, i.e. the two samples come from the same distribution, is reject with confidence level \(\alpha = 5\%\).
KS-test on a non-stationary time series
# ============== Setups ==============
set.seed(2) # random seed
ci <- 0.05 # confidence level (alpha)
n <- 500 # number of simulations
# Simulated non-stationary sample
x1 <- rnorm(n/2, 0, 1)
x2 <- rnorm(n/2, 0.3, 1)
x <- c(x1, x2)
# ====================================
# Random split of the time series
t_split <- sample(n, 1)
x1 <- x[1:t_split]
x2 <- x[(t_split+1):n]
# Number of elements for each sub sample
n1 <- length(x1)
n2 <- length(x2)
# Grid of values for KS-statistic
grid <- seq(quantile(x, 0.015), quantile(x, 0.985), 0.01)
# Empiric cdfs
cdf_1 <- ecdf(x1)
cdf_2 <- ecdf(x2)
# KS-statistic
ks_stat <- max(abs(cdf_1(grid) - cdf_2(grid)))
# Rejection level
rejection_lev <- sqrt(-0.5*log(ci/2))*sqrt((n1+n2)/(n1*n2))
# P-value
p.value <- exp(- (2 * n2) / (1 + n1/n2) * ks_stat^2)KS-test plot
y_breaks <- seq(0, 1, 0.2)
y_labels <- paste0(format(y_breaks*100, digits = 2), "%")
grid_max <- grid[which.max(abs(cdf_1(grid) - cdf_2(grid)))]
ggplot()+
geom_ribbon(aes(grid, ymax = cdf_1(grid), ymin = cdf_2(grid)),
alpha = 0.5, fill = "green") +
geom_line(aes(grid, cdf_1(grid)))+
geom_line(aes(grid, cdf_2(grid)), color = "red")+
geom_segment(aes(x = grid_max, xend = grid_max,
y = cdf_1(grid_max), yend = cdf_2(grid_max)),
linetype = "solid", color = "magenta")+
geom_point(aes(grid_max, cdf_1(grid_max)), color = "magenta")+
geom_point(aes(grid_max, cdf_2(grid_max)), color = "magenta")+
scale_y_continuous(breaks = y_breaks, labels = y_labels)+
labs(x = "x", y = "cdf")+
theme_bw()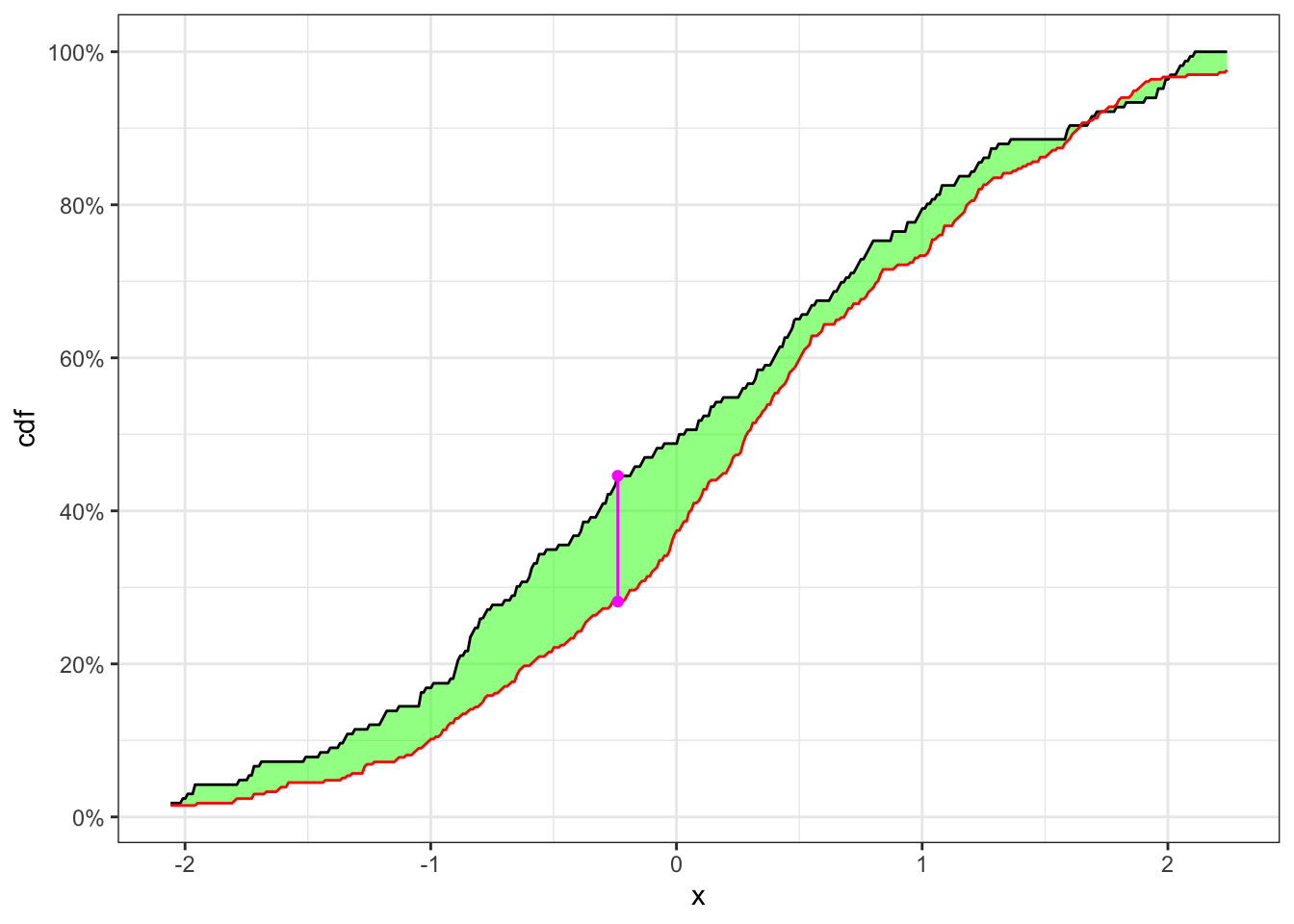
| \(\textbf{Index split}\) | \(\alpha\) | \(n_1\) | \(n_2\) | \(\text{KS}(\mathbf{x}_{n_1}, \mathbf{x}_{n_2})\) | p.value | \(\textbf{Critical level}\) | \(\mathcal{H}_0\) |
|---|---|---|---|---|---|---|---|
| 166 | 0.05 | 166 | 334 | 0.1643 | 0.000005831 | 0.129 | Rejected |
