20 ARMA processes
20.1 ARMA(p, q)
An Auto Regressive Moving Average processes, or for short ARMA(p,q), is a combination of an MA(q) (Equation 19.1) and an AR(p) (Equation 19.3), i.e. \[ Y_t = \mu + \sum_{i=1}^{p}\phi_{i} Y_{t-i} + \sum_{j=1}^{q}\theta_{j} u_{t-j} + u_{t} \text{,} \tag{20.1}\] where in general \(u_t \sim \text{WN}(0, \sigma_{\text{u}}^2)\) (Definition 18.5).
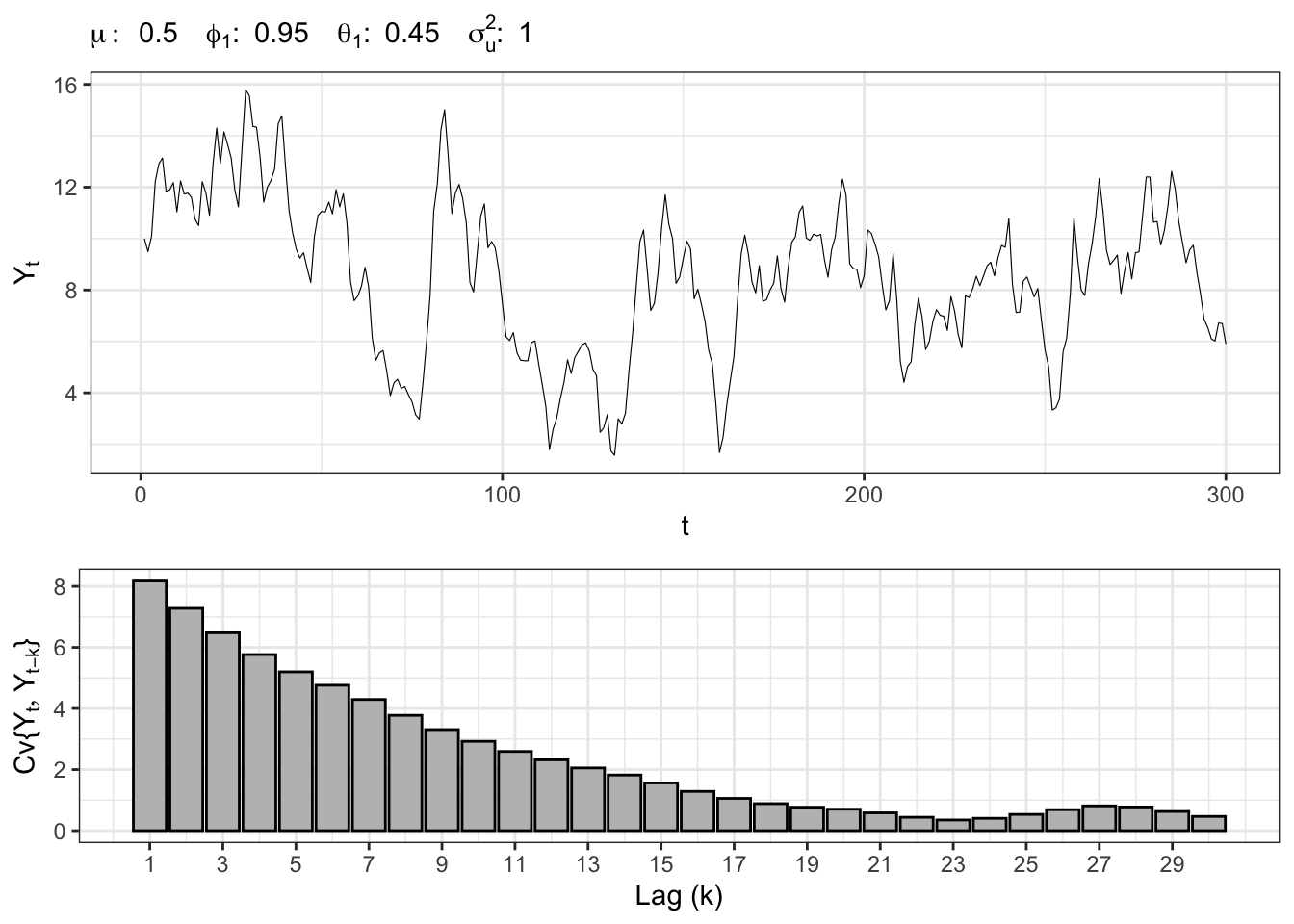
ARMA(1,1) simulation
set.seed(6) # random seed
# *************************************************
# Inputs
# *************************************************
# Number of steps ahead
t_bar <- 300
# Intercept
mu <- 0.5
# AR parameters
phi <- c(phi1 = 0.95)
# MA parameters
theta <- c(theta1 = 0.45)
# Variance of the residuals
sigma2_u <- 1
# *************************************************
# Simulations
# *************************************************
# Initial value
Yt <- c(mu / (1 - phi[1]))
# Simulated residuals
u_t <- rnorm(t_bar, 0, sqrt(sigma2_u))
# Simulated ARMA(1,1)
for(t in 2:t_bar){
# AR component
sum_AR <- phi[1] * Yt[t-1]
# MA component
sum_MA <- theta[1] * u_t[t-1]
# Update Yt
Yt[t] <- mu + sum_AR + sum_MA + u_t[t]
}
20.1.1 Matrix form
An Autoregressive process of order p AR(p) (Equation 19.3) can be written in matrix form as \[ \mathbf{Y}_t = \mathbf{c} + \mathbf{\Phi} \mathbf{Y}_{t-1} + \mathbf{b} \, u_t \text{,} \] where \[ \underset{\mathbf{Y}_t}{ \underbrace{ \begin{pmatrix} Y_t \\ Y_{t-1} \\ \vdots \\ Y_{t-p} \end{pmatrix} }} = \underset{\mathbf{c}}{ \underbrace{ \begin{pmatrix} \mu \\ 0 \\ \vdots \\ 0 \end{pmatrix} }} + \underset{\boldsymbol{\Phi}}{ \underbrace{ \begin{pmatrix} \phi_1 & \phi_2 & \dots & \phi_{p-1} & \phi_p \\ 1 & 0 & \dots & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & 1 & 0 \\ 0 & 0 & \dots & 0 & 0 \end{pmatrix} }} \underset{\mathbf{Y}_{t-1}}{ \underbrace{ \begin{pmatrix} Y_{t-1} \\ Y_{t-2} \\ \vdots \\ Y_{t-p-1} \end{pmatrix} }} + \underset{\mathbf{b}}{ \underbrace{ \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} }} \cdot u_t \] where \(\mathbf{Y}_t\), \(\mathbf{c}\) and \(\mathbf{b}\) have dimension \(p \times 1\), while \(\boldsymbol{\Phi}\) is \(p \times p\).
Let’s consider the vector containing the coefficients of the model, i.e. \[ \underset{p \times 1}{\boldsymbol{\gamma}} = \begin{pmatrix} \phi_1 & \phi_2 & \dots & \phi_{p-1} & \phi_p \end{pmatrix} \text{.} \] If the order of the Autoregressive process is greater than 1, i.e. \(p > 1\), let’s consider an identity matrix (Equation 31.3) with dimension \((p-1) \times (p-1)\), i.e. \[ \mathbf{I}_{p-1} = \begin{pmatrix} 1 & 0 & \dots & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & 1 & 0 \\ 0 & 0 & \dots & 0 & 1 \end{pmatrix} \text{,} \] and combine it with a column of zeros, i.e. \[ \underset{(p-1) \times p}{\mathbf{L}} = \begin{pmatrix} \mathbf{I}_{p-1} & \mathbf{0}_{1\times (p-1)} \end{pmatrix} \text{.} \] Finally, add on the top of \(\mathbf{L}\) with the AR parameters, i.e. \[ \underset{p \times p}{\mathbf{\Phi}} = \begin{pmatrix} \boldsymbol{\gamma} \\ \mathbf{L} \end{pmatrix} \text{.} \]
Example 20.1 Let’s consider an AR(4) process of the form \[ Y_t = \mu + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \phi_3 Y_{t-3} + \phi_4 Y_{t-4} + u_t \text{.} \] Then, the vector containing the coefficients of the model reads \[ \underset{4 \times 1}{\boldsymbol{\gamma}} = \begin{pmatrix} \phi_1 & \phi_2 & \phi_{3} & \phi_4 \end{pmatrix} \text{.} \]
For an AR(4) we start with a diagonal matrix with dimension \(3 \times 3\), i.e. \[ \mathbf{I}_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \text{,} \] and we add a column of zeros, i.e. \[ \underset{3 \times 4}{\mathbf{L}_3} = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \text{.} \] and the parameters \[ \underset{4 \times 4}{\mathbf{\Phi}} = \begin{pmatrix} \phi_1 & \phi_2 & \phi_{3} & \phi_4 \\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \text{.} \] In order to verify the above result, let’s consider the iteration from \(t-1\) to time \(t\), in matrix form one obtain \[ \begin{pmatrix} Y_t \\ Y_{t-1} \\ Y_{t-2} \\ Y_{t-3} \end{pmatrix} = \begin{pmatrix} \mu \\ 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} \phi_1 & \phi_2 & \phi_{3} & \phi_4 \\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} Y_{t-1} \\ Y_{t-2} \\ Y_{t-3} \\ Y_{t-4} \end{pmatrix} + \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} u_t \text{.} \] After an explicit computation, one can verify that it lead to the classic AR(4) recursion, i.e. \[ \begin{aligned} \begin{pmatrix} Y_t \\ Y_{t-1} \\ Y_{t-2} \\ Y_{t-3} \\ \end{pmatrix} {} & = \begin{pmatrix} \mu \\ 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \phi_3 Y_{t-3} + \phi_4 Y_{t-4} \\ Y_{t-1} \\ Y_{t-2} \\ Y_{t-3} \\ \end{pmatrix} + \begin{pmatrix} u_t \\ 0 \\ 0 \\ 0 \\ \end{pmatrix} \end{aligned} \]
Let’s now consider the matrix form an ARMA (p,q) process (Equation 20.1), i.e. \[ \mathbf{X}_t = \mathbf{c} + \mathbf{A} \mathbf{X}_{t-1} + \mathbf{b} u_t \text{,} \] where, the first component, namely \(Y_t = \mathbf{e}_{p+q}^{\top} \mathbf{X}_t\), is extracted as: \[ Y_t = \mathbf{e}_{p+q}^{\top} \mathbf{c} + \mathbf{e}_{p+q}^{\top} \mathbf{A} \mathbf{X}_{t-1} + \mathbf{e}_{p+q}^{\top} \mathbf{b} \, u_t \text{.} \] where \(\mathbf{e}_{p+q}^{\top}\) is a basis vector (Equation 31.1) with dimension \(p+q\).
\[ \underset{\mathbf{X}_t}{ \underbrace{ \begin{pmatrix} Y_t \\ Y_{t-1} \\ \vdots \\ Y_{t-p} \\ u_{t} \\ u_{t-1} \\ \vdots \\ u_{t-q} \end{pmatrix} }} = \underset{\mathbf{c}}{ \underbrace{ \begin{pmatrix} \mu \\ 0 \\ 0 \\ \vdots \\ 0 \\ 0 \end{pmatrix} }} + \underset{\mathbf{A}}{ \underbrace{ \begin{pmatrix} \phi_1 & \phi_2 & \dots & \phi_{p-1} & \phi_p & \theta_1 & \theta_2 & \dots & \theta_{q-1} & \theta_q \\ 1 & 0 & \dots & 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & 1 & 0 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 0 & 0 & 0 & \dots & 1 & 0 \end{pmatrix} }} \underset{\mathbf{X}_{t-1}}{ \underbrace{ \begin{pmatrix} Y_{t-1} \\ Y_{t-2} \\ \vdots \\ Y_{t-p-1} \\ u_{t-1} \\ u_{t-2} \\ \vdots \\ u_{t-p-1} \end{pmatrix} }} + \underset{\mathbf{b}}{ \underbrace{ \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} }} \cdot u_t \]
Let’s consider the vector \(\gamma\) containing the coefficients of the model, i.e. \[ \underset{1 \times (q+p)}{\boldsymbol{\gamma}} = \begin{pmatrix} \phi_1 & \phi_2 & \dots & \phi_{p-1} & \phi_p & \theta_1 & \theta_2 & \dots & \theta_{q-1} & \theta_q \end{pmatrix} \text{.} \] For an ARMA(p,q) we consider two distinct matrices, i.e. a matrix for the AR part we consider the identity matrix (Equation 31.3) with order \(p-1\), i.e. \[ \underset{(p-1) \times (p-1)}{\mathbf{I}_{p-1}} = \begin{pmatrix} 1 & 0 & \dots & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & 1 & 0 \\ 0 & 0 & \dots & 0 & 1 \end{pmatrix} \text{,} \] and we combine it with a column of zeros, i.e. \[ \underset{(p-1) \times p}{\mathbf{L}^{\tiny \text{AR}}} = \begin{pmatrix} \mathbf{I}_{p-1} & \mathbf{0}_{(p-1) \times 1} \end{pmatrix} = \begin{pmatrix} 1 & 0 & \dots & 0 & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & 0 \\ 0 & 0 & \dots & 1 & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 & 0 \end{pmatrix} \text{.} \] For the MA part we consider the identity matrix with order \(q-1\), i.e. \[ \mathbf{I}_{q-1} = \begin{pmatrix} 1 & 0 & \dots & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & 1 & 0 \\ 0 & 0 & \dots & 0 & 1 \end{pmatrix} \text{,} \] and we combine it with a column of zeros, i.e. \[ \underset{(q-1) \times q}{\mathbf{L}^{\tiny \text{MA}}} = \begin{pmatrix} \mathbf{I}_{q-1} & \mathbf{0}_{(q-1) \times 1} \end{pmatrix} = \begin{pmatrix} 1 & 0 & \dots & 0 & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & 0 \\ 0 & 0 & \dots & 1 & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 & 0 \end{pmatrix} \text{.} \] To combine the matrices \(\mathbf{L}_{p-1}\) and \(\mathbf{L}_{q-1}\), we need add a matrix of zeros. More precisely: \[ \underset{(q+p-1) \times (q+p)}{\mathbf{L}} = \begin{pmatrix} \mathbf{L}^{\tiny \text{AR}} & \mathbf{0}_{(p-1) \times q } \\ \mathbf{0}_{1 \times p} & \mathbf{0}_{1 \times q} \\ \mathbf{0}_{(q-1) \times p} & \mathbf{L}^{\tiny \text{MA}} \end{pmatrix} \text{.} \] Finally we combine \(\mathbf{L}\) with the parameters, i.e. \[ \underset{(q+p) \times (q+p)}{\mathbf{A}} = \begin{pmatrix} \boldsymbol{\gamma} \\ \mathbf{L} \end{pmatrix} \text{.} \] Then, the vector \(\mathbf{b}\) is constructed by combining two basis vectors (Equation 31.1), to ensure it is equal to one in the position 1 and in the position p+1, i.e. \[ \mathbf{b} = \begin{pmatrix} \mathbf{e}_p \\ \mathbf{e}_q \end{pmatrix} \text{.} \]
Example 20.2 For example let’s consider an ARMA(2,3): \[ \boldsymbol{\gamma} = \begin{pmatrix} \phi_1 & \phi_2 & \theta_1 & \theta_2 & \theta_3 \end{pmatrix} \text{.} \] The matrix for the AR part that is equal to \(\mathbf{\Phi}\) combined with a matrix of zeros, i.e. \[ \underset{1 \times 2}{\mathbf{L}^{\tiny \text{AR}}} = \begin{pmatrix} 1 & 0 \end{pmatrix} \text{,} \] For the MA part we consider a similar matrix as in the single case but with first row equal to zero, i.e. \[ \underset{2 \times 3}{\mathbf{L}^{\tiny \text{MA}}} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix} \text{,} \] and we combine \[ \underset{4 \times 5}{\mathbf{L}} = \begin{pmatrix} \mathbf{L}^{\tiny \text{AR}} & \mathbf{0}_{2 \times 3} \\ \mathbf{0}_{1 \times 2} & \mathbf{0}_{1 \times 3} \\ \mathbf{0}_{2 \times 2} & \mathbf{L}^{\tiny \text{MA}} \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} \text{.} \] Finally we combine \[ \underset{5 \times 5}{\mathbf{A}} = \begin{pmatrix} \boldsymbol{\gamma}\\ \mathbf{L} \end{pmatrix} = \begin{pmatrix} \phi_1 & \phi_2 & \theta_1 & \theta_2 & \theta_3 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} \text{.} \] Then, the vector \(\mathbf{b}\) is constructed by combining two vectors \[ \mathbf{b} = \begin{pmatrix} \mathbf{e}_2 \\ \mathbf{e}_3 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 \end{pmatrix}^{\top} \text{.} \] Let’s check it would lead to a classic ARMA(2,3): \[ \begin{aligned} \begin{pmatrix} Y_t \\ Y_{t-1} \\ u_t \\ u_{t-1} \\ u_{t-2} \\ \end{pmatrix} & {} = \begin{pmatrix} \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \theta_1 u_{t-1} + \theta_2 u_{t-1} + \theta_2 u_{t-2} \\ Y_{t-1} \\ 0 \\ u_{t-1} \\ u_{t-2} \\ \end{pmatrix} + \begin{pmatrix} u_t \\ 0 \\ u_t \\ 0 \\ 0 \\ \end{pmatrix} \\ & = \begin{pmatrix} \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \theta_1 u_{t-1} + \theta_2 u_{t-1} + \theta_3 u_{t-2} + u_t \\ Y_{t-1} \\ u_t \\ u_{t-1} \\ u_{t-2} \\ \end{pmatrix} \end{aligned} \]
20.2 Moments
Proposition 20.1 Given the information at time \(t\), the forecasted value at time \(t+h\) for an AR(p) process reads: \[ \mathbf{X}_{t+h} = \sum_{j = 0}^{h-1} \mathbf{A}^j \mathbf{c} + \mathbf{A}^h \mathbf{X}_{t} + \sum_{j = 0}^{h-1} \mathbf{A}^j \mathbf{b} \, u_{t+h-j} \text{.} \tag{20.2}\]
Proposition 20.2 (\(\color{magenta}{\textbf{Expectation of an ARMA}}\))
The conditional expectation at time \(t+h\) of \(\mathbf{X}_{t+h}\) given the information up to time \(t\) can be easily computed from Equation 20.2, i.e. \[
\mathbb{E}\{\mathbf{X}_{t+h}\mid \mathcal{F}_t \} = \mathbf{c} \ (\mathbf{I}_p - \mathbf{A}^h) \ (\mathbf{I}_p - \mathbf{A})^{-1} + \mathbf{A}^h \mathbf{X}_{t}
\text{.}
\]
Proposition 20.3 (\(\color{magenta}{\textbf{Variance of an ARMA}}\))
Taking the variance of Equation 20.2 on both sides gives \[
\mathbb{V}\{\mathbf{X}_{t+h}\mid \mathcal{F}_t \} = \sigma_{\text{u}}^2 \sum_{j = 0}^{h-1} \mathbf{A}^j \mathbf{b} \mathbf{b}^{\top} (\mathbf{A}^j)^{\top}
\text{.}
\] Moreover, Assuming \(u_t \sim \text{WN}(0, \sigma_{\text{u}}^2)\), and independence across time, the conditional covariance is: \[
\mathbb{C}v\{\mathbf{X}_{t+h}, \mathbf{X}_{t+k} \mid \mathcal{F}_t \} = \sigma_{\text{u}}^2 \sum_{j=0}^{\min(h,k)-1}
\mathbf{A}^{h-1-j} \mathbf{b} \mathbf{b}^{\top} (\mathbf{A}^{k-1-j})^{\top}.
\]
Example 20.3 Let’s use Monte Carlo simulations to establish if the results are accurate.
simulate_ARMA
# Simulate an ARMA(p, q) process
simulate_ARMA <- function(t_bar, nsim = 1, mu = 0, phi = c(0.5, 0.2), theta = c(0.4, 0.1), sigma2 = 1, y0, eps0){
scenarios <- list()
# MA order
q <- length(theta)
# AR order
p <- length(phi)
# Initial lag to start
i_start <- max(c(p, q)) + 1
for(sim in 1:nsim){
# Simulated residuals
if (!missing(eps0)){
eps <- c(eps0, rnorm(t_bar - q, sd = sqrt(sigma2)))
} else {
eps <- rnorm(t_bar, sd = sqrt(sigma2))
}
# Initialize the simulation
if (!missing(y0)){
x <- c(y0)
} else {
x <- eps
}
for(t in i_start:t_bar){
# AR part
ar_part <- 0
for(i in 1:length(phi)){
ar_part <- ar_part + phi[i] * x[t-i]
}
# MA part
ma_part <- 0
for(i in 1:length(theta)){
ma_part <- ma_part + theta[i] * eps[t-i]
}
# Next step simulation
x[t] <- mu + ar_part + ma_part + eps[t]
}
scenarios[[sim]] <- x
}
scenarios
}ARMA moments
# *************************************************
# Inputs
# *************************************************
set.seed(6) # random seed
nsim <- 200 # Number of simulations
t_bar <- 100000 # Steps for each simulation
phi <- c(0.3, 0.15) # AR parameters
theta <- c(0.3, 0.15, 0.1) # MA parameters
mu <- 0.3 # Intercept
sigma2 <- 1 # Variance of the residuals
y0 <- c(0.9, 0.2, 0) # Initial values for y0
eps0 <- c(0.3, -0.2, 0.1) # Initial values for eps0
h <- 200 # Number of steps ahead
# *************************************************
# Simulations
# *************************************************
scenarios <- simulate_ARMA(t_bar, nsim, mu, phi, theta,
sigma2, y0, eps0)
# Build companion matrix
L_AR <- matrix(c(1, 0, 0, 0, 0), nrow = 1)
L_MA <- cbind(c(0, 0), c(0, 0), diag(2), c(0, 0))
A <- rbind(c(phi, theta), L_AR, rep(0, 5), L_MA)
# Build vector b
b <- matrix(c(1, 0, 1, 0, 0), ncol = 1)
# Build vector c
c <- matrix(c(mu, 0, 0, 0, 0), ncol = 1)
# *************************************************
# Moments
# *************************************************
# Compute expectation and variances with Monte Carlo
e_mc <- mean(purrr::map_dbl(scenarios, ~mean(.x)))
v_mc <- mean(purrr::map_dbl(scenarios, ~var(.x)))
cv_mc_L1 <- mean(purrr::map_dbl(scenarios, ~cov(.x[-1], lag(.x, 1)[-1])))
cv_mc_L2 <- mean(purrr::map_dbl(scenarios, ~cov(.x[-c(1,2)], lag(.x, 2)[-c(1,2)])))
cv_mc_L3 <- mean(purrr::map_dbl(scenarios, ~cov(.x[-c(1:3)], lag(.x, 3)[-c(1:3)])))
cv_mc_L4 <- mean(purrr::map_dbl(scenarios, ~cov(.x[-c(1:4)], lag(.x, 4)[-c(1:4)])))
cv_mc_L5 <- mean(purrr::map_dbl(scenarios, ~cov(.x[-c(1:5)], lag(.x, 5)[-c(1:5)])))
# Compute expectation and variances with Formula
# State vector for forecasting
X0 = c(y0[-3][c(2,1)], eps0[c(3:1)])
e_mod <- expectation_ARMA(X0, h = h, A, b, c)[1,1]
v_mod <- covariance_ARMA(h, h, A, b, sigma2)[1,1]
cv_mod_L1 <- covariance_ARMA(h, h-1, A, b, sigma2 = 1)[1,1]
cv_mod_L2 <- covariance_ARMA(h, h-2, A, b, sigma2 = 1)[1,1]
cv_mod_L3 <- covariance_ARMA(h, h-3, A, b, sigma2 = 1)[1,1]
cv_mod_L4 <- covariance_ARMA(h, h-4, A, b, sigma2 = 1)[1,1]
cv_mod_L5 <- covariance_ARMA(h, h-5, A, b, sigma2 = 1)[1,1]| Covariance | Formula | MonteCarlo |
|---|---|---|
| \(\mathbb{E}\{Y_t\}\) | 0.5454545 | 0.5451268 |
| \(\mathbb{V}\{Y_t\}\) | 1.7466575 | 1.7472189 |
| \(\mathbb{C}v\{Y_t, Y_{t-1}\}\) | 1.1317615 | 1.1322251 |
| \(\mathbb{C}v\{Y_t, Y_{t-2}\}\) | 0.8115271 | 0.8118819 |
| \(\mathbb{C}v\{Y_t, Y_{t-3}\}\) | 0.5132223 | 0.5133504 |
| \(\mathbb{C}v\{Y_t, Y_{t-4}\}\) | 0.2756958 | 0.2758340 |
| \(\mathbb{C}v\{Y_t, Y_{t-5}\}\) | 0.1596921 | 0.1596755 |
