30  Exponential distribution

Figure 30.1: Distribution (left) and density (right) functions of an Exponential random variable.

An exponential random variable $X$ is defined only on the positive real line, i.e. $X\in [0,\mathrm{\infty }]$, and its distribution depends on a parameter $\lambda >0$ called rate.

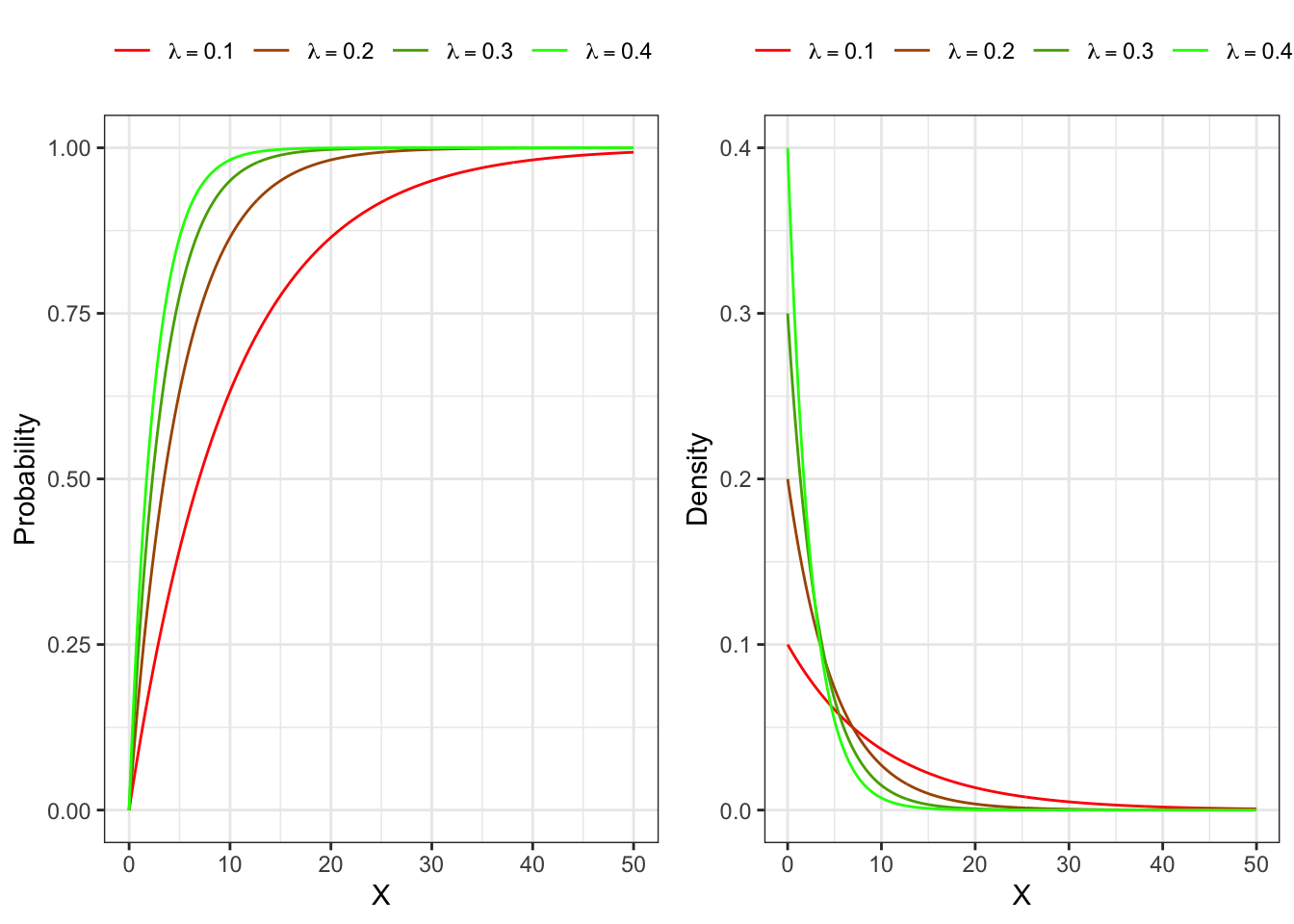
30.1 Distribution

The distribution function of an exponential random variable reads $$\begin{array}{}\text{(30.1)}& F_X(x)=1-e^{-\lambda x}\text{,}x\in [0,\mathrm{\infty }]\text{.}\end{array}$$ Symmetrically the survival function ${\overline{F}}_X(x)=1-F_X(x)$ $${\overline{F}}_X(x)=e^{-\lambda x}\text{,}x\in [0,\mathrm{\infty }]\text{.}$$ Taking the derivative with respect to $x$ of Equation 30.1 gives the density function, i.e. $$f_X(x)=\lambda e^{-\lambda x}\text{,}x\in [0,\mathrm{\infty }]\text{,}$$

30.2 Quantile

The quantile function of an exponential random variable is defined as $$q_X(\alpha )=-\frac{1}{\lambda }\log (1-\alpha )\text{,}\alpha \in [0,1]\text{,}$$

Proof. The quantile function of a random variable is implicitly defined as the level of $X=q_X(\alpha )$ such that the distribution function computed in $q_X(\alpha )$ gives a probability equal to $\alpha$. More precisely, one must solve for $q_X(\alpha )$ such that: $$\alpha =F_X(q_X(\alpha ))=1-e^{-\lambda q_X(\alpha )}⟹q_X(\alpha )=-\frac{1}{\lambda }\log (1-\alpha )$$