Reference: Chapter 1. Resnick (2005).
In probability, an event is interpreted as a collection of possible outcomes of a random experiment.
Definition 1.1 ()
A random experiment is any repeatable procedure that results in one out of a well-defined set of possible outcomes.
- The set of possible outcomes is called sample space and denoted with . An element of is denoted as and is an outcome
- A set of zero or more outcomes is an event , where we denote with a class of subsets .
- A map (function) that goes from the space of the events to the space of probabilities (real numbers in ) is the probability law and is denoted with .
Together, sample space, event space and probability law characterize a random experiment.
There are several definitions related to sets and their operation.
Definition 1.2 ()
The complement of a set is denoted by and represents the set of elements that do not belong to , i.e.
Definition 1.3 ()
A set is said to be contained in a set if every element of is also an element of . Formally,
Definition 1.4 ()
Given two sets, is equal to , written , if and only if every element of is an element of and every element of is an element of . Formally,
Set operations
Let’s now state some elementary operations between sets.
Definition 1.5 ()
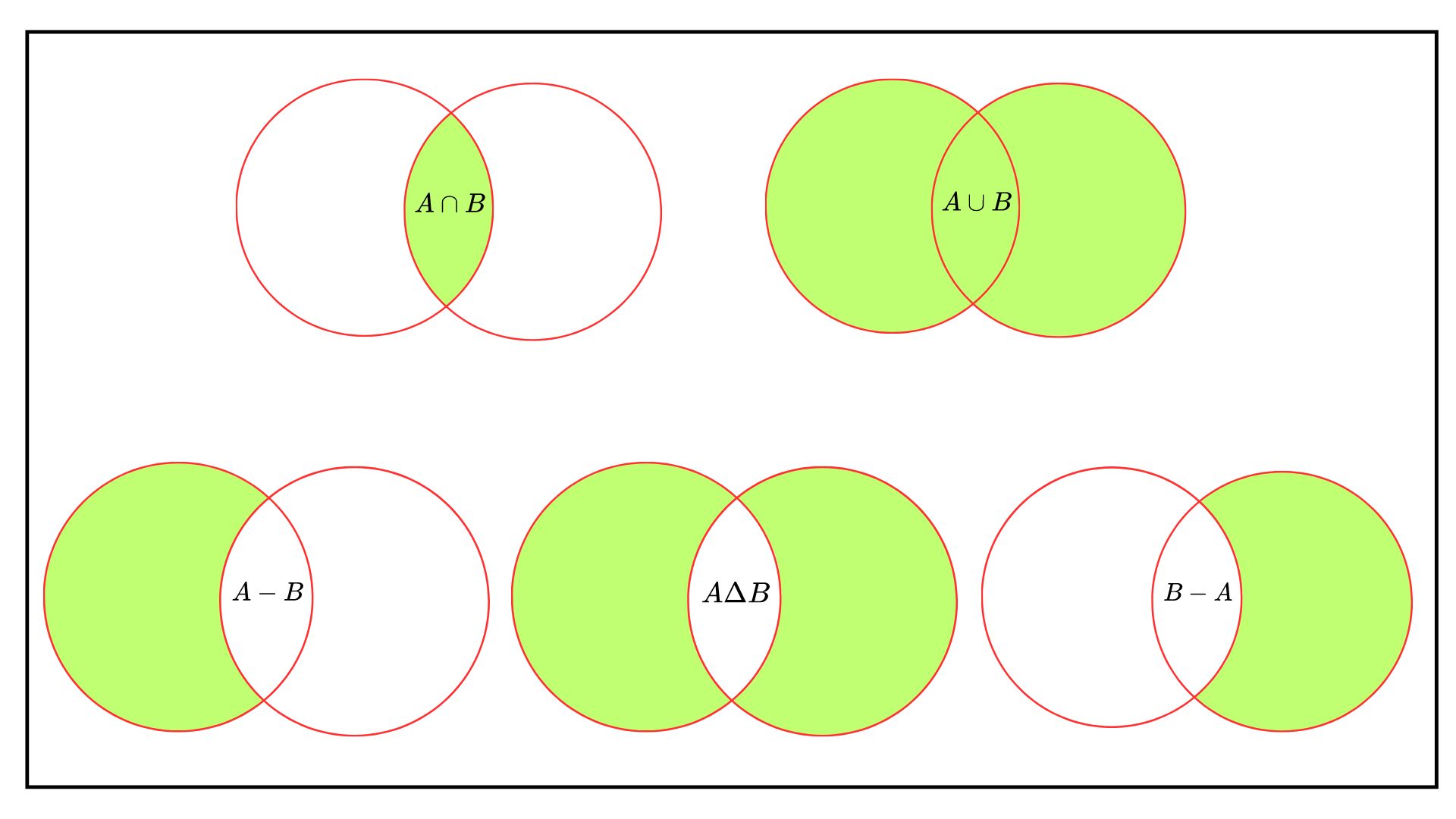
The union of two sets, written , is the set of that belongs either to or , i.e.
As a consequence of the definition of the union the following relations holds true, i.e.
Definition 1.6 ()
The intersection of and is written and is the set of elements that belongs at the same time to and .
As a consequence of the definition of the intersection the following relations holds, i.e. Moreover, let’s state the distributive laws of the union and the intersection, i.e. And the De Morgan’s laws:
Definition 1.7 ()
The difference between two sets and , written (or also ), is the set of elements of that do not belong to . Formally
Given two set and , then each one can be written as the union of disjoint sets. In fact, their union can be decomposed into the union of three disjoint sets, i.e. and therefore for example the set can be written as
Definition 1.8 ()
The symmetric difference between two sets and is written and is the union of elements of that do not belong to and of elements of that do not belong to , i.e.
Proposition 1.1 Given two set , the symmetric difference can be written as
Proof. Let’s denote with , then apply the distributive law of the union twice (Equation 1.5) and develop the computations, i.e.
Indicator function
Definition 1.9 ()
An indicator function is a function that associate an to a real number, i.e. either 0 or 1. It is a tool that allows to transfer a computation from the set domain into the real numbers domain, i.e. . Formally, , i.e.
Proposition 1.2 The containment between two sets can be equivalently written in terms of indicator functions:
Proof. Let’s start by assuming and let’s distinguish two main cases.
- Assuming implies that , and therefore one have an equality .
- Assuming implies . In this situation for both cases one will have that , in fact:
- Considering implies that .
- Considering implies that .
Hence, assuming implies that for all . Now let’s assume the contrary: and let’s again distinguish in two main cases:
- Assuming , i.e. , the inequality holds and since the indicator function is bounded by 1 by definition it is possible to write . Therefore, one obtain and so .
- Assuming , i.e. , the inequality holds and it is possible to write . Hence, when , there are two possible cases, i.e.
- , but this implies that .
- , but this implies that .
When an implies that , but the contrary do not holds true. Hence, it is possible to conclude that .
Limits of sets
Let’s define the infimum () and the supremum () of a sequence of sets as Informally, the infimum of a sequence of sets is the smallest set in , on the other hand, the supremum of a sequence of sets is the biggest set in .
Then, the is defined as The liminf (limit inferior of sets) is the set of all elements that eventually always belong to the sequence . By definition, the limit of the infimum () is the biggest (union) among all the smallest (intersection) sets. In other words, if there exists some index such that for all , we have .
Instead, the is defined as The limsup (limit superior of sets) is the set of all elements that belong infinitely often to the sequence . By definition, the limit of the supremum () is the smallest (intersection) among all the biggest (union) sets. In other words, if for infinitely many , .
Monotone Sequences
Let’s define a sequence of sets as monotone non-decreasing if , while we define it monotone non-increasing if . In general, a monotone non-decreasing sequence is denoted with , while a non-increasing one with . In general, the limit of a monotone sequence always exists.
Definition 1.10 ()
Let’s consider a monotone sequence of sets . Then, if
is a sequence of non-decreasing sets, i.e. , then the limit exists, i.e.
is a sequence of non-increasing sets, i.e. , then the limit exists, i.e.
Fields and -fields
Definition 1.11 ()
Let’s define a field as a non-empty class of subsets of closed under complementation, finite union and intersection. The minimal requirements for a class of subsets to be a field are:
- , i.e. the sample space if in .
- , i.e. if a set is in , then also its complement is in .
- , i.e. if two sets and are in , then also their union (or intersection) is in .
Definition 1.12 ()
Let’s define a -field as a non-empty class of subsets of closed under complementation, countable union and intersection. The minimal requirements for a class of subsets to be a -field are:
- , i.e. the sample space if in .
- , i.e. if a set is in , then also its complement is in .
- , i.e. if a countable sequence of sets is in , then also its countable union (or intersection) is in .
The main difference between a field and a -field is in the third property of the definitions. A field is closed under finite union, namely the union of a finite sequence of events indexed by (property 3 of Definition 1.11). On the other hand, a -field is closed under countable union, namely the union of an infinite sequence of events indexed by (property 3. of the Definition 1.12).
Exercise 1.1 Let the sample space be . Generate a -algebra according to Definition 1.12
Solution 1.1. Let the sample space be . A natural choice of –algebra on a finite set is the power set:
Resnick, Sidney I. 2005.
A Probability Path. Birkhauser.
https://link.springer.com/book/10.1007/978-0-8176-8409-9.