26  Stationarity tests

library(dplyr)
library(knitr)
library(ggplot2)

26.1 Dickey–Fuller test

The Dickey–Fuller test tests the null hypothesis that a unit root is present in an auto regressive (AR) model. The alternative hypothesis is different depending on which version of the test is used, usually is “stationary” or “trend-stationary”. Let’s consider an AR(1) model, i.e. $$\begin{array}{}\text{(26.1)}& x_t=\mu +\delta t+{\varphi }_1{x}_{t-1}+u_t\text{,}\end{array}$$ or equivalently adding and subtracting $x_{t-1}$ $$\begin{array}{}\text{(26.2)}& \mathrm{\Delta }{x}_t=\mu +\delta t+(1-{\varphi }_1)x_{t-1}+u_t\text{.}\end{array}$$ The hypothesis of the Dickey–Fuller test are: $$\begin{array}{rl}& {\text{H}}_0:{\varphi }_1=1(\text{non stationarity})\\ & {\text{H}}_1:{\varphi }_1<1(\text{stationarity})\end{array}$$ The Dickey–Fuller statistic (DF) is computed as: $$\text{DF}=\frac{1-{\varphi }_1}{\mathbb{S}d\{1-{\varphi }_1\}}$$ However, since the test is done over the residual term rather than raw data, it is not possible to use the t-distribution to provide critical values. Therefore, the statistic $DF$ has a specific distribution.

26.2 Augmented Dickey–Fuller test

The augmented Dickey–Fuller is a more general version of the Dickey–Fuller test for a general AR(p) model, i.e.  $$\mathrm{\Delta }{x}_t=\mu +\delta t+\gamma x_{t-1}+\sum _{i=1}^p{\varphi }_i\mathrm{\Delta }{x}_{t-i}$$ The hypothesis of the augmented Dickey–Fuller test are: $$\begin{array}{rl}& {\text{H}}_0:\gamma =0(\text{non stationarity})\\ & {\text{H}}_1:\gamma <0(\text{stationarity})\end{array}$$ The augmented Dickey–Fuller statistic (ADF) is computed as: $$\text{ADF}=\frac{\gamma }{\mathbb{S}d\{\gamma \}}$$ As in the simpler case, the critical values are computed using a specific table for the Dickey–Fuller test.

26.3 Kolmogorov-Smirnov test

The Kolmogorov–Smirnov two-sample test (KS) can be used to test whether two samples came from the same distribution. Let’s define the empirical distribution function $F_n$ of $n$-independent and identically distributed ordered observations $X_{(i)}$ as $$F_n(x)=\frac{1}{n}\sum _{i=1}^n{\mathbb{1}}_{(-\mathrm{\infty },x]}(X_{(i)})\text{.}$$ The KS statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution functions of two random samples. The distribution of the KS statistic under the null hypothesis assumes that the samples are drawn from the same distribution, i.e.  $$\begin{array}{rl}& {\text{H}}_0:X\text{is stationary}\\ & {\text{H}}_1:X\text{is not stationary}\end{array}$$ The statistic test for two samples with dimension $n_1$ and $n_2$ is defined as: $${\text{KS}}_{n_1,n_2}=\underset{\mathrm{\forall }x}{sup}|F_{n_1}(x)-F_{n_2}(x)|\text{,}$$ and for large samples $H_0$ is rejected with confidence level $1-\alpha$ if: $${\text{KS}}_{n_1,n_2}>\sqrt{-\frac{1}{2n_2}\ln \left(\frac{\alpha }{2}\right)(1+\frac{n_2}{n_1})}\text{.}$$ Hence, since the statistic is always greater of equal to zero, with a given statistic ${\text{KS}}_{n_1,n_2}$ the p-value with confidence level $\alpha =2\mathbb{P}(X>{\text{KS}}_{n_1,n_2})$ reads: $$\mathbb{P}(X>{\text{KS}}_{n_1,n_2})=\exp (-\frac{2n_2}{1+\frac{n1}{n2}}{\text{KS}}_{n_1,n_2}^2)$$

KS test for time series

To apply the test in a time series settings, use a random index to split the original series in two sub-series. Then the KS can be applied as usual.

26.3.1 Examples

Check for stationarity

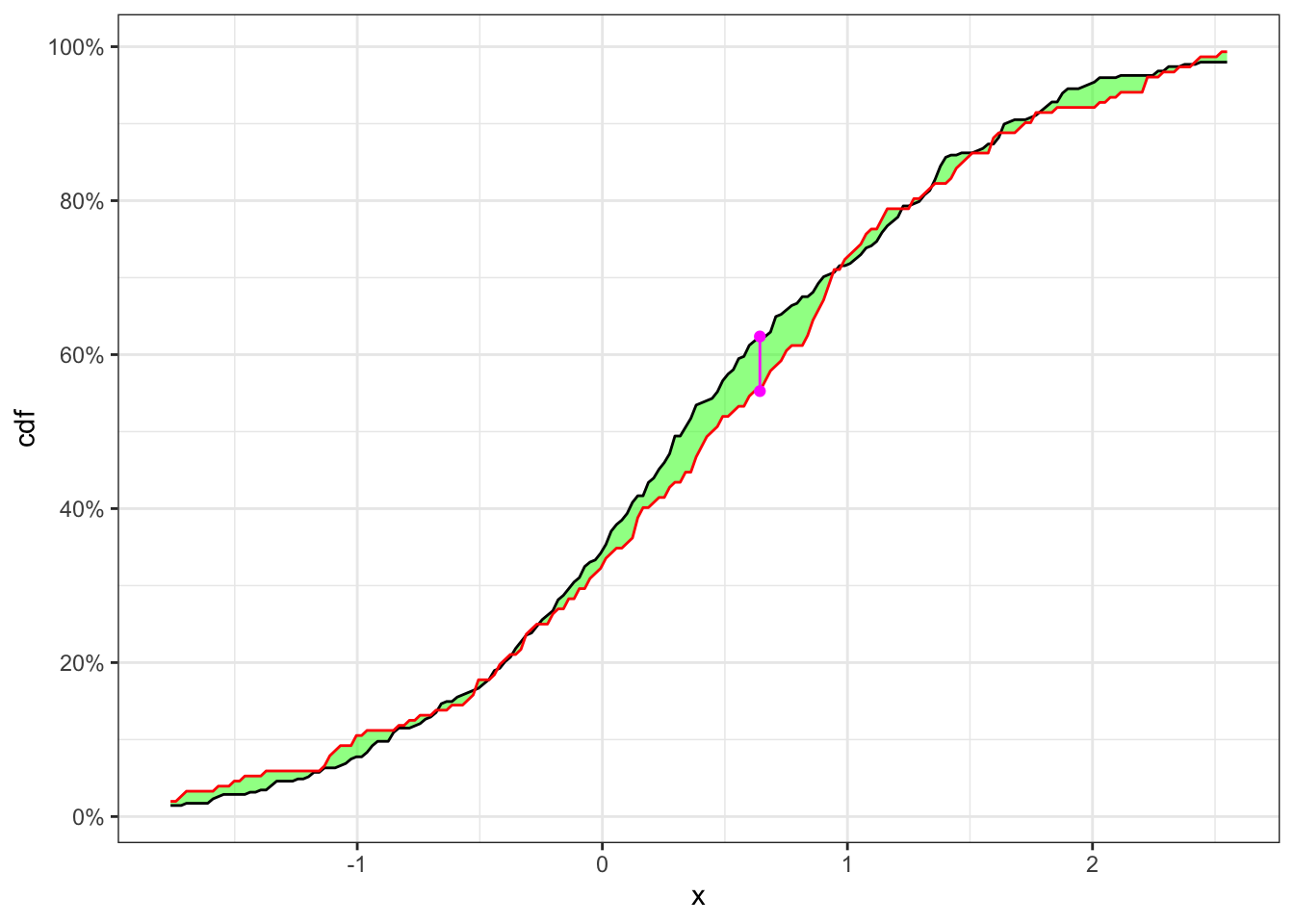
Example 26.1 Let’s consider 500 simulated observations of the random variable $X$ drown from a population distributed as $X\sim N(0.4,1)$. Then, considering it as a time series, let’s sample a random index to split the series in a point. Finally, as shown in Table 26.1 the null hypothesis, i.e. the two samples come from the same distribution, is not reject with the confidence level $\alpha =5\mathrm{\%}$.

# ================ Setups ================
set.seed(5) # random seed
ci <- 0.05  # confidence level (alpha)
n <- 500    # number of simulations
x <- rnorm(n, 0.4, 1) # stationary series 
# ========================================
# Random time for splitting 
t_split <- sample(n, 1)
# Split the time series
x1 <- x[1:t_split]
x2 <- x[(t_split+1):n]
# Number of elements for each sub-series 
n1 <- length(x1)
n2 <- length(x2)
# Grid of values for computing KS-statistic
x_min <- quantile(x, 0.015)
x_max <- quantile(x, 0.985)
grid <- seq(x_min, x_max, length.out = 200)
# Empirical cdfs 
cdf_n1 <- ecdf(x1)
cdf_n2 <- ecdf(x2)
# KS-statistic 
ks_stat <- max(abs(cdf_n1(grid) - cdf_n2(grid)))
# Rejection level with probability alpha 
rejection_lev <- sqrt(-0.5*log(ci/2))*sqrt((n1+n2)/(n1*n2))
# P-value
p.value <- exp(- (2 * n2) / (1 + n1/n2) * ks_stat^2)

y_breaks <- seq(0, 1, 0.2)
y_labels <- paste0(format(y_breaks*100, digits = 2), "%")
grid_max <- grid[which.max(abs(cdf_n1(grid) - cdf_n2(grid)))]
ggplot()+
  geom_ribbon(aes(grid, ymax = cdf_n1(grid), ymin = cdf_n2(grid)), 
              alpha = 0.5, fill = "green") +
  geom_line(aes(grid, cdf_n1(grid)))+
  geom_line(aes(grid, cdf_n2(grid)), color = "red")+
  geom_segment(aes(x = grid_max, xend = grid_max, y = cdf_n1(grid_max), yend = cdf_n2(grid_max)), 
               linetype = "solid", color = "magenta")+
  geom_point(aes(grid_max, cdf_n1(grid_max)), color = "magenta")+
  geom_point(aes(grid_max, cdf_n2(grid_max)), color = "magenta")+
  scale_y_continuous(breaks = y_breaks, labels = y_labels)+
  labs(x = "x", y = "cdf")+
  theme_bw()

Figure 26.1: Two samples cdfs and KS-statistic (magenta) for a stationary time series.

kab <- tibble(
  t_split = t_split,
  ci = ci,
  n1 = n1,
  n2 = n2,
  KS = ks_stat,
  p.value = p.value,
  rejection_lev = rejection_lev,
  H0 = ifelse(KS > rejection_lev, "Rejected", "Non-Rejected")
)  %>%
  mutate_if(is.numeric, format, digits = 4, scientific = FALSE)
colnames(kab) <- c("$\\textbf{Index split}$","$\\alpha$", "$n_1$", "$n_2$", 
                   "$KS_{n_1, n_2}$", "p.value", "$\\textbf{Critical level}$", "$H_0$")
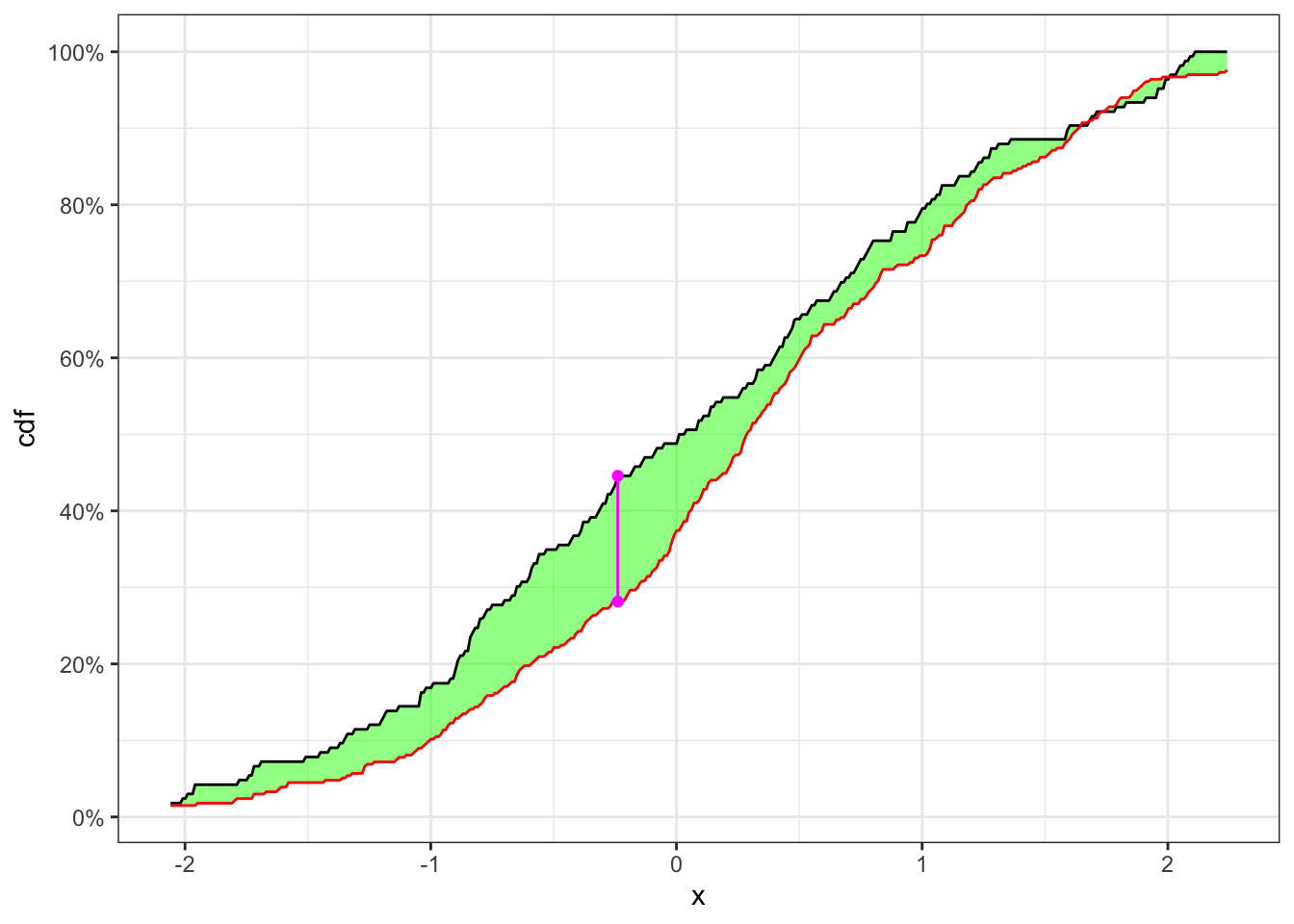
knitr::kable(kab, escape = FALSE)

Table 26.1: KS test for a stationary time series.

$\mathbf{\text{Index split}}$	$\alpha$	$n_1$	$n_2$	$K{S}_{n_1,n_2}$	p.value	$\mathbf{\text{Critical level}}$	$H_0$
348	0.05	348	152	0.07093	0.6282	0.132	Non-Rejected

Check for non-stationarity

Example 26.2 Let’s consider 250 simulated observations of the random variable $X$ drown from a population distributed as $Y_{1,t}\sim N(0,1)$ and the following 250 from $Y_{2,t}\sim N(0.3,1)$. Then the non-stationary series will have a structural break at the point 250 and the time series is given by: $$X_t=\{\begin{array}{l}{Y}_{1,t}t\le 250\\ Y_{2,t}t>250\end{array}$$ As in Example 26.2 let’s split the time series and apply the KS-test. In this case, as shown in Table 26.2 the null hypothesis, i.e. the two samples come from the same distribution, is reject with confidence level $\alpha =5\mathrm{\%}$.

# ============== Setups ==============
set.seed(2) # random seed
ci <- 0.05  # confidence level (alpha)
n <- 500    # number of simulations
# Simulated non-stationary sample 
x1 <- rnorm(n/2, 0, 1)
x2 <- rnorm(n/2, 0.3, 1)
x <- c(x1, x2)
# ====================================
# Random split of the time series
t_split <- sample(n, 1)
x1 <- x[1:t_split]
x2 <- x[(t_split+1):n]
# Number of elements for each sub sample 
n1 <- length(x1)
n2 <- length(x2)
# Grid of values for KS-statistic
grid <- seq(quantile(x, 0.015), quantile(x, 0.985), 0.01)
# Empiric cdfs 
cdf_1 <- ecdf(x1)
cdf_2 <- ecdf(x2)
# KS-statistic 
ks_stat <- max(abs(cdf_1(grid) - cdf_2(grid)))
# Rejection level  
rejection_lev <- sqrt(-0.5*log(ci/2))*sqrt((n1+n2)/(n1*n2))
# P-value
p.value <- exp(- (2 * n2) / (1 + n1/n2) * ks_stat^2)

y_breaks <- seq(0, 1, 0.2)
y_labels <- paste0(format(y_breaks*100, digits = 2), "%")
grid_max <- grid[which.max(abs(cdf_1(grid) - cdf_2(grid)))]
ggplot()+
  geom_ribbon(aes(grid, ymax = cdf_1(grid), ymin = cdf_2(grid)), 
              alpha = 0.5, fill = "green") +
  geom_line(aes(grid, cdf_1(grid)))+
  geom_line(aes(grid, cdf_2(grid)), color = "red")+
  geom_segment(aes(x = grid_max, xend = grid_max, 
                   y = cdf_1(grid_max), yend = cdf_2(grid_max)), 
               linetype = "solid", color = "magenta")+
  geom_point(aes(grid_max, cdf_1(grid_max)), color = "magenta")+
  geom_point(aes(grid_max, cdf_2(grid_max)), color = "magenta")+
  scale_y_continuous(breaks = y_breaks, labels = y_labels)+
  labs(x = "x", y = "cdf")+
  theme_bw()

Figure 26.2: Two samples cdfs and KS-statistic (magenta) for a non-stationary time series.

kab <- dplyr::tibble(
  t_split = t_split,
  ci = ci,
  n1 = n1,
  n2 = n2,
  KS = ks_stat,
  p.value = p.value,
  rejection_lev = rejection_lev,
  H0 = ifelse(KS > rejection_lev, "Rejected", "Non-Rejected"))  %>%
  mutate_if(is.numeric, format, digits = 4, scientific = FALSE)
colnames(kab) <- c("$\\textbf{Index split}$","$\\alpha$", "$n_1$", "$n_2$", 
                   "$KS_{n_1, n_2}$", "p.value", "$\\textbf{Critical level}$", "$H_0$")
knitr::kable(kab, escape = FALSE) 

Table 26.2: KS test for a non-stationary time series.

$\mathbf{\text{Index split}}$	$\alpha$	$n_1$	$n_2$	$K{S}_{n_1,n_2}$	p.value	$\mathbf{\text{Critical level}}$	$H_0$
166	0.05	166	334	0.1643	0.000005831	0.129	Rejected